रेखाओं का समीकरण (Equation of lines)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Equation of lines, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• निर्देशांक ज्यामिति क्या होती है?
• निर्देशांक ज्यामिति में निर्देशांक और बिंदुओं की स्थिति ढूँढना
• रेखाओं का समीकरण
• निर्देशांक ज्यामिति - दो रेखाएं
• त्रिभुज
• चतुर्भुज
• वृत्त का समीकरण
• बिंदु का प्रतिबिंब

रेने डेसकार्टेस (René Descartes) ने प्रस्तावित किया कि निर्देशांक ज्यामिति का उपयोग करके, समीकरणों द्वारा भी रेखाओं (और वक्रों का भी) का वर्णन किया जा सकता है।

आइए देखें कैसे।

X और Y अक्षों का समीकरण (Equation of X and Y axes)

हम बहुत ही बुनियादी अवधारणाओं से शुरू करेंगे।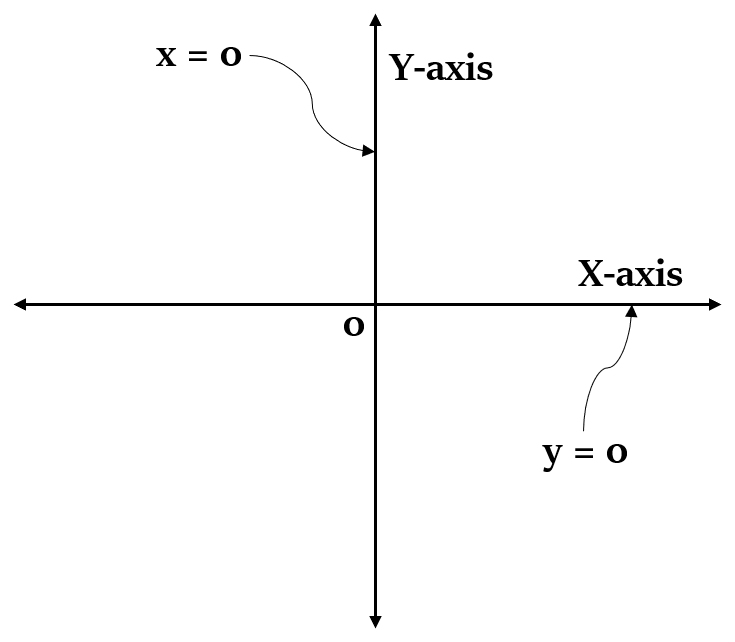

Coordinate Geometry

• Y-अक्ष का समीकरण x = 0 है
• X-अक्ष का समीकरण y = 0 है

X और Y अक्षों के समानांतर रेखाओं का समीकरण (Equation of lines parallel to X and Y axes)

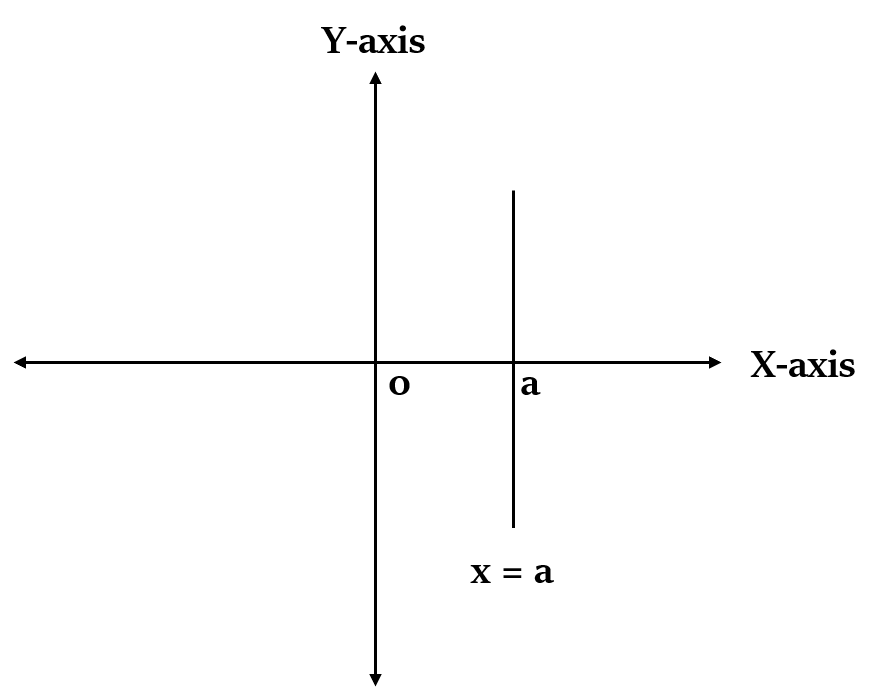
• Y-अक्ष के समांतर रेखा का समीकरण x = a होता है
  

  Coordinate Geometry

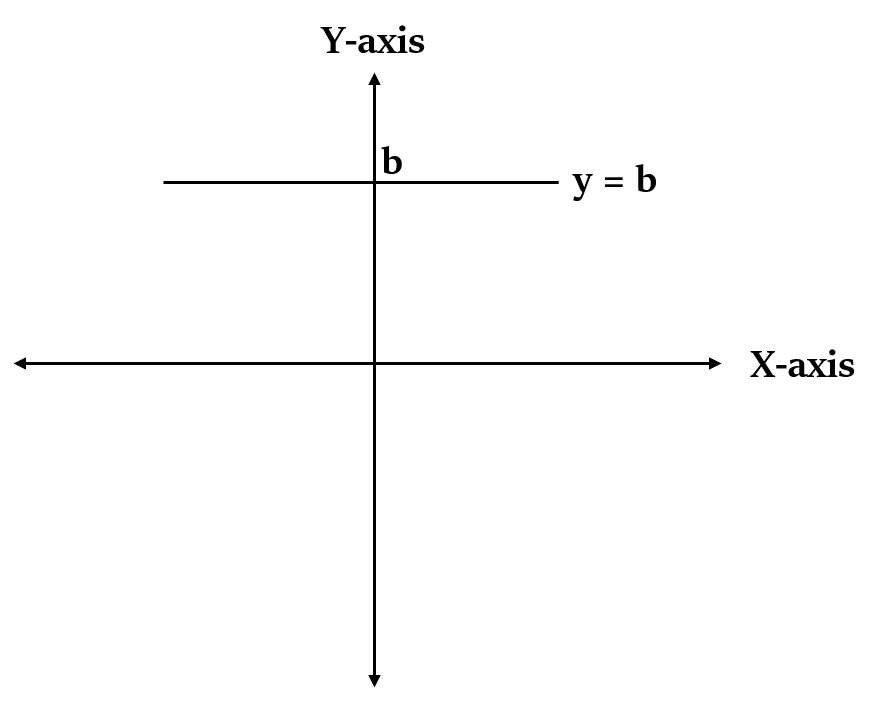
• X-अक्ष के समांतर रेखा का समीकरण y = b होता है
  

  Coordinate Geometry

a, b कोई अचर (constants) हैं।

सामान्य रेखाओं का समीकरण (Equation of general lines)

सीधी रेखा का सामान्य समीकरण ax + by + c = 0 होता है, जहाँ x और y चर (variables) हैं और a, b और c अचर (constants) हैं।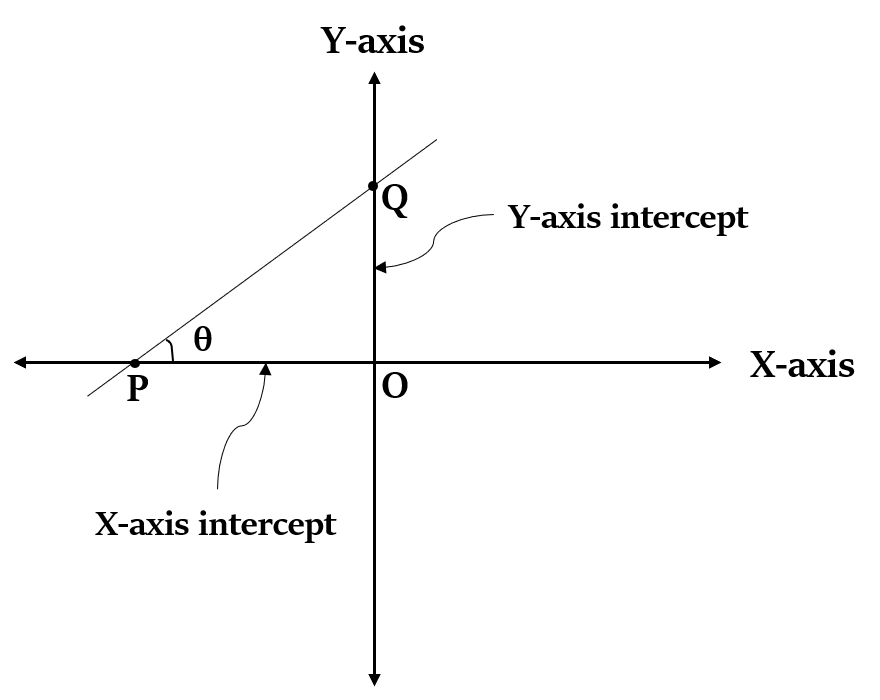

Coordinate Geometry

रेखा पर स्थित कोई भी बिंदु उस रेखा के समीकरण को संतुष्ट करेगा। अर्थात्, यदि हम रेखा के समीकरण में उस बिंदु के निर्देशांक डाल दें, तो समीकरण के बाएँ हाथ और दाएँ हाथ के हिस्से बराबर होंगे।

रेखा समीकरणों के संबंध में कुछ ऐसे शब्द हैं, जिनसे हमें अवगत होना चाहिए।

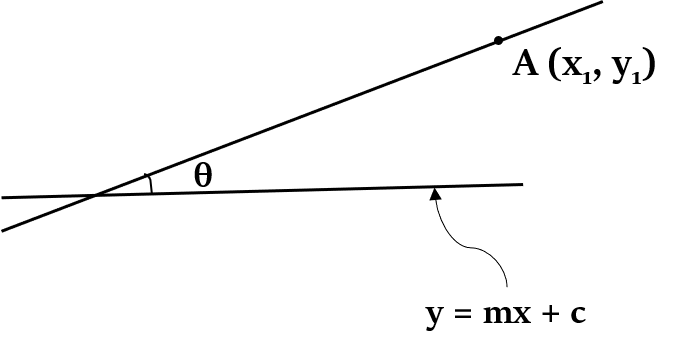
झुकाव और ढलान का कोण (Angle of inclination and Slope) - एक रेखा X-अक्ष के साथ घड़ी की विपरीत दिशा में जो कोण बनाती है, उसे उस रेखा का झुकाव कहा जाता है। ऊपर दी गई आकृति में, रेखा PQ X-अक्ष के साथ θ का कोण बनाती है। रेखा का ढाल tan θ होगा।

अक्ष पर अंतःखंड (Intercepts on Axes) - वो बिंदु जहां कोई रेखा एक अक्ष को काटती है, और मूल निर्देशांक (origin) के बीच की दूरी को उस विशेष अक्ष पर उस रेखा का अंतःखंड (Intercept) कहा जाता है। ऊपर दिए गए चित्र में, OP और OQ क्रमशः X-अक्ष अंतःखंड और Y-अक्ष अंतःखंड हैं, जो रेखा PQ द्वारा बनाए गए हैं।

नोट

हम समीकरण ax + by + c = 0 को निम्न प्रकार से फिर से लिख सकते हैं:
y = $-\frac{a}{b} x - \frac{c}{b}$

रेखा का ढलान (slope), m = tan θ = $-\frac{a}{b}$

• एक रेखा की ढलान को हमेशा वामावर्त दिशा (anticlockwise direction) में मापा जाता है।
• यदि ढाल = ∞ हो, तो वह रेखा y-अक्ष के समांतर या x-अक्ष के लंबवत होती है।
• यदि ढलान = 0 है, तो वह रेखा x-अक्ष के समानांतर या y-अक्ष के लंबवत होती है।

अब, ऐसे कई तरीके हैं जिनसे हम किसी दी गई रेखा के समीकरण को निरूपित कर सकते हैं। आइए, इन सभी रूपों को समझते हैं।

रेखा समीकरणों के विभिन्न रूप (Various forms of Line Equations)

प्रतिच्छेद रूप (Intercept Form)

यदि किसी रेखा का X-प्रतिच्छेदन और Y-प्रतिच्छेदन क्रमशः a और b हैं, तो रेखा का समीकरण होगा: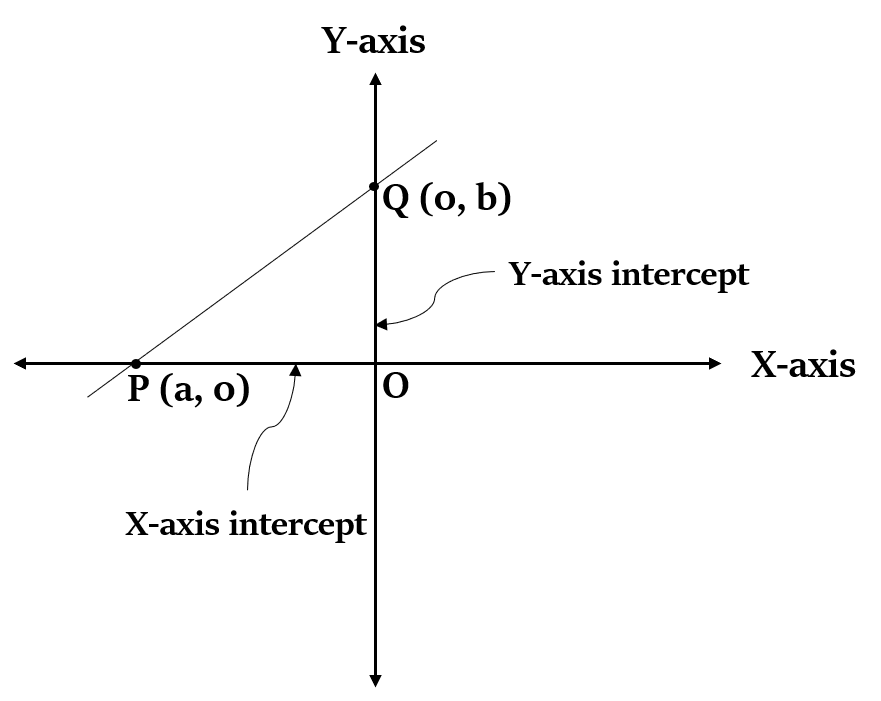

Coordinate Geometry

$\frac{x}{a} + \frac{y}{b}$ = 1

दो अक्षों के बीच अंतःखंड (intercept) की लंबाई = $\sqrt{a^2 + b^2}$

ढलान प्रतिच्छेद रूप (Slope Intercept Form)

यदि किसी रेखा का Y-प्रतिच्छेदन c है, और रेखा का ढलान m है, तो रेखा का समीकरण होगा: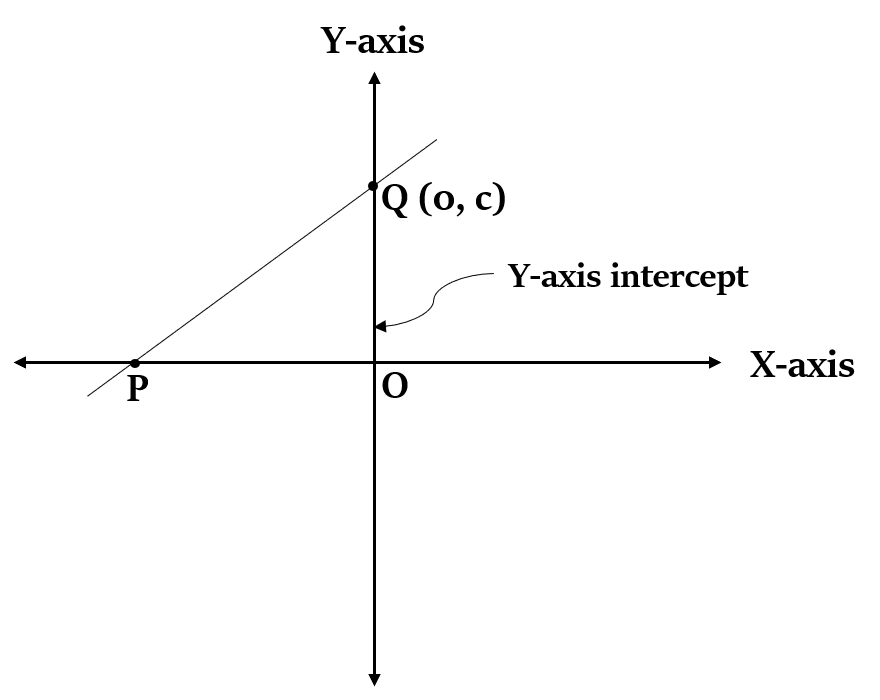

Coordinate Geometry

y = mx + c

उदाहरण के लिए, y = 2x + 3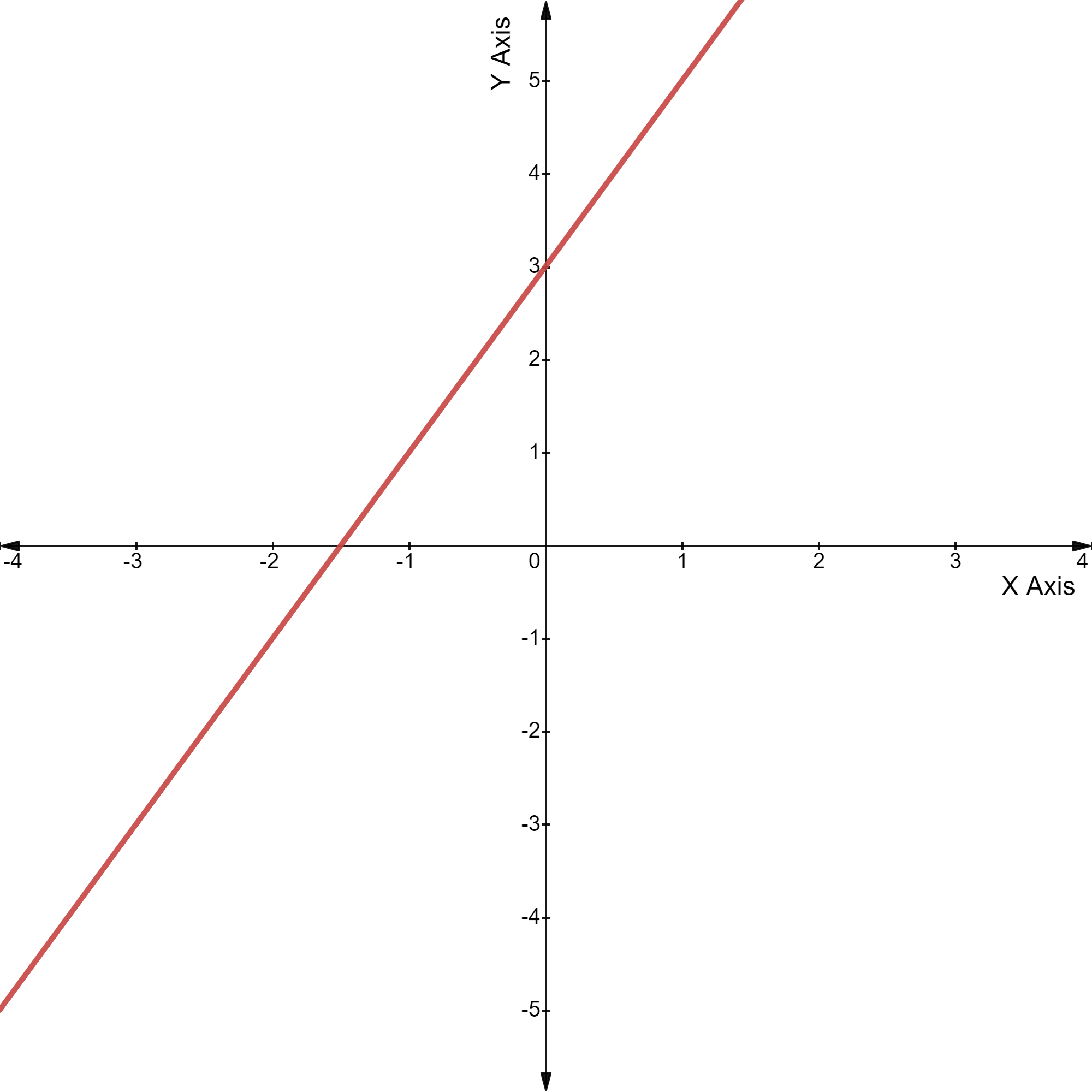

Coordinate Geometry

नोट

यदि रेखा मूल निर्देशांक से होकर गुजरती है, तो c = 0.

अतः, ऐसी रेखा का समीकरण होगा, y = mx

उदाहरण के लिए, y = 2x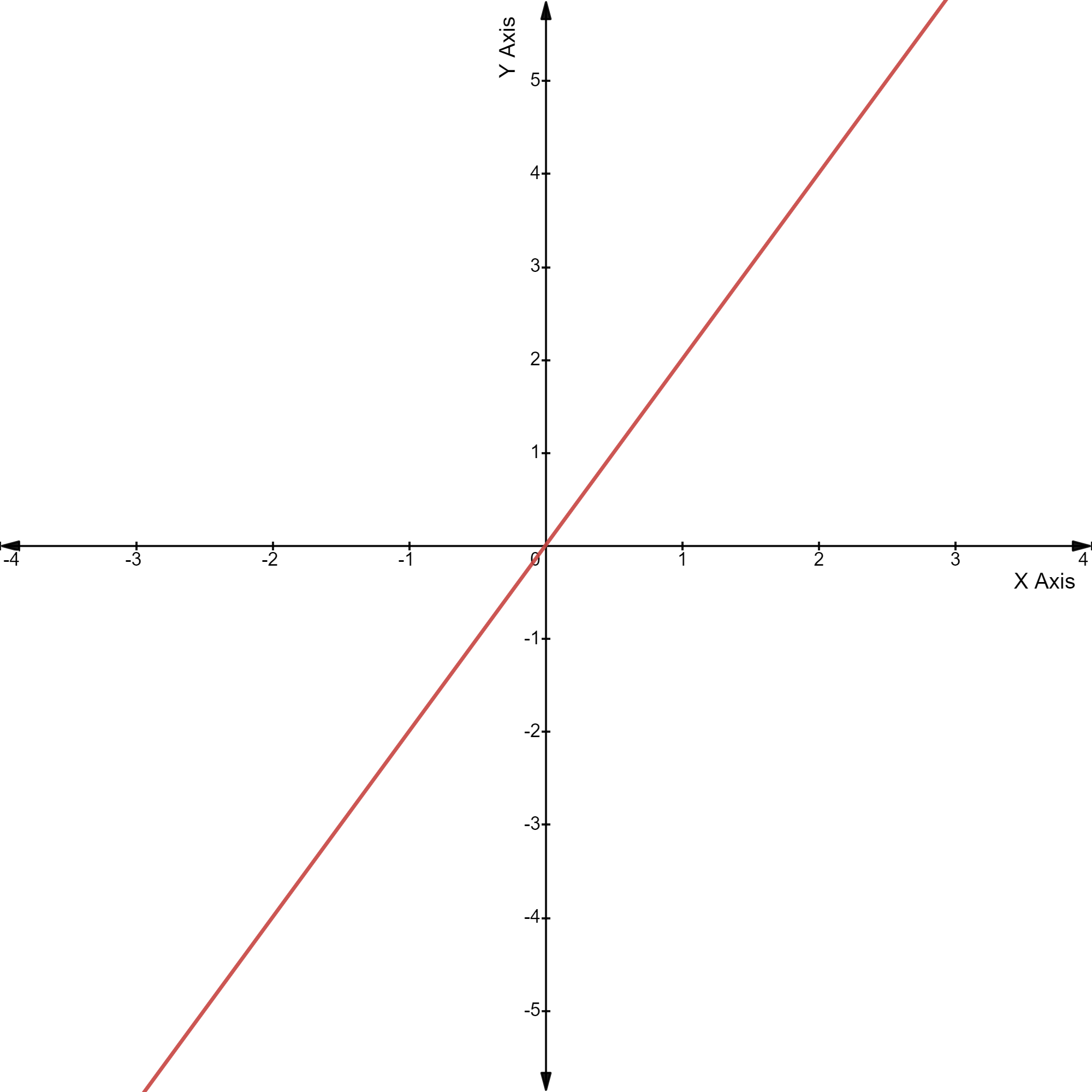

Coordinate Geometry

बिंदु ढलान रूप (Point Slope Form)

यदि कोई रेखा बिंदु $(x_1, y_1)$ से होकर गुजरती है और रेखा का ढलान m है, तो रेखा का समीकरण होगा:

आरेख: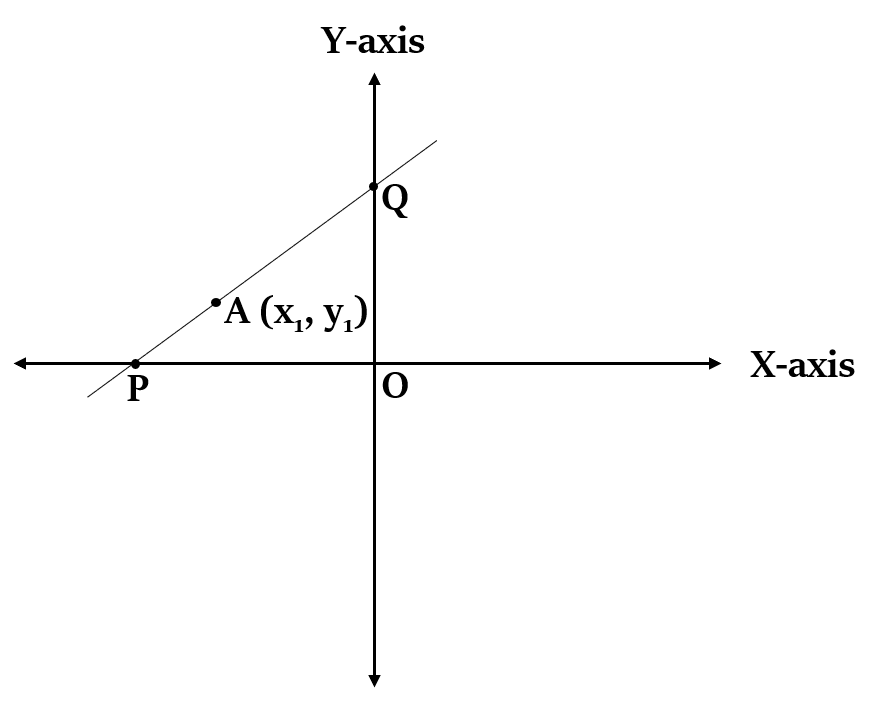

Coordinate Geometry

$(y – y_1) = m(x – x_1)$

दो बिंदु रूप (Two Points Form)

यदि कोई रेखा दो बिंदुओं $(x_1, y_1)$, और $(x_2, y_2)$ से होकर गुजरती है, तो रेखा का समीकरण होगा:

आरेख: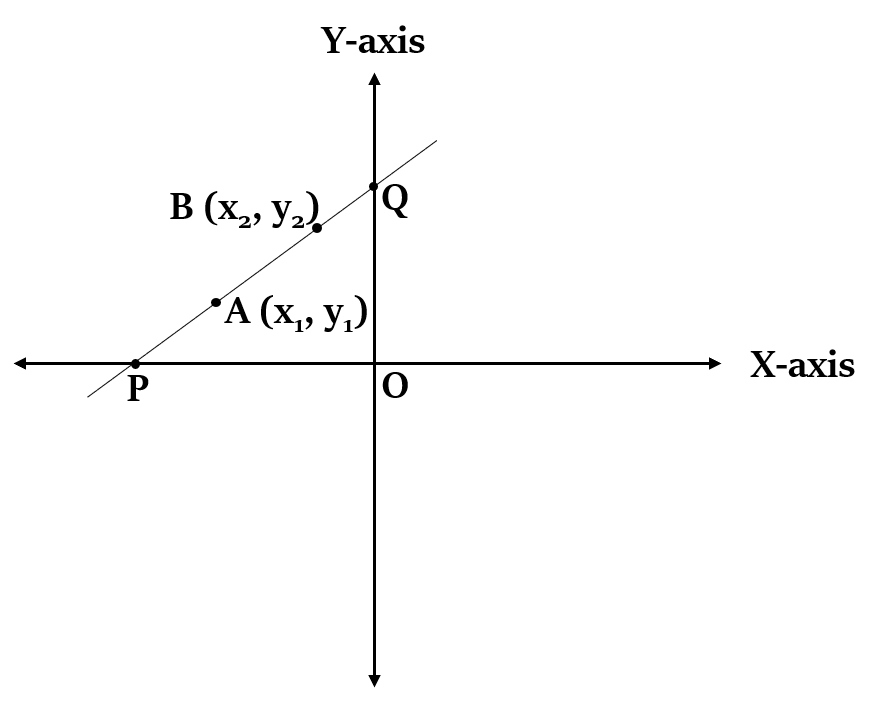

Coordinate Geometry

$(y – y_1) = \frac{y_2 – y_1}{x_2 – x_1} (x – x_1)$

जहाँ, रेखा की ढलान, m = $\frac{y_2 – y_1}{x_2 – x_1}$

Normal Form

यदि मूल निर्देशांक से किसी रेखा पर लम्ब की लंबाई 'p' है, और यह लम्बवत रेखा X-अक्ष की धनात्मक दिशा से θ का कोण बनाती है, तो रेखा का समीकरण होगा: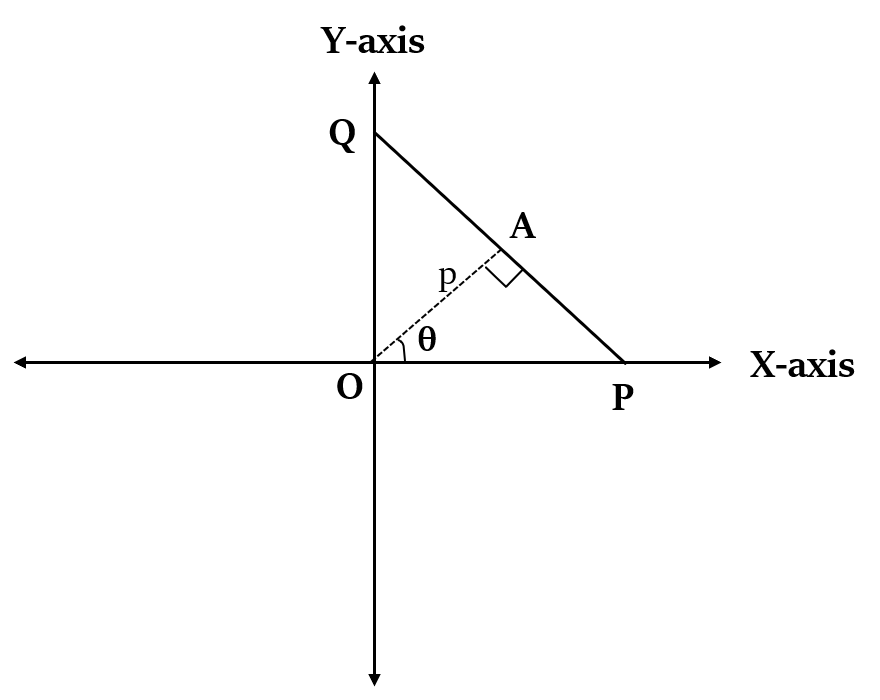

Coordinate Geometry

x cos θ + y sin θ = p

Parametric Form

It is also called as Distance/Symmetrical Form.

यदि कोई रेखा X-अक्ष की धनात्मक दिशा के साथ θ का कोण बनाती है, और वह बिंदुओं (x, y) और ($x_1, y_1$) से गुजरती है, जो r इकाई अलग हैं, तो रेखा का समीकरण होगा:

आरेख: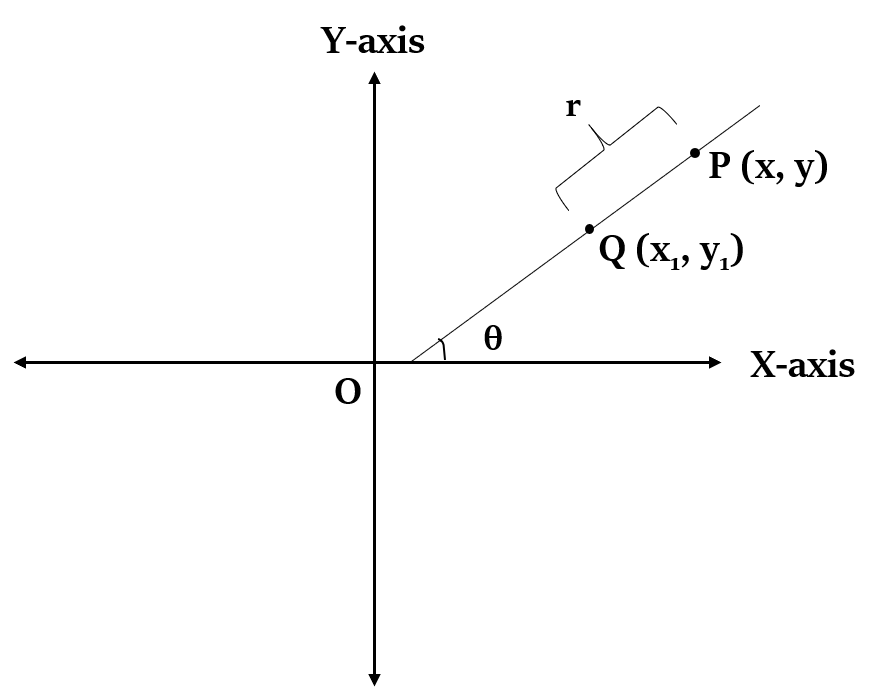

Coordinate Geometry

$\frac{x - x_1}{cos θ} = \frac{y - y_1}{sin θ}$ = r

बिंदु P के निर्देशांक होंगे: ($x_1 + r cos θ, y_1 + r sin θ$)

अन्य रेखाओं के सापेक्ष रेखाओं का समीकरण (Equation of Lines with respect to other lines)

हम पहले ही विभिन्न तरीकों को देख चुके हैं, जिनसे हम किसी रेखा का समीकरण लिख सकते हैं। इस लेख में हम सीखेंगे कि बहु-रेखाओं (multiple lines) के समीकरण कैसे लिखे जाते हैं।

एक रेखा का दूसरी रेखा के सापेक्ष समीकरण (Equation of a line with respect to another line)

सीधी रेखा के समीकरण जो एक बिंदु A ($x_1$, $y_1$) से होकर गुजरती हैं, और रेखा y = mx + c के साथ θ का कोण बनाती हैं:

आरेख:

Coordinate Geometry

$y - y_1 = \frac{m \hspace{1ex} ± \hspace{1ex} tan θ}{1 \hspace{1ex} ∓ \hspace{1ex} m \hspace{1ex} tan θ} (x - x_1)$

दो अन्य रेखाओं के सापेक्ष किसी रेखा का समीकरण (Equation of a line with respect to two other lines)

प्रतिच्छेदन बिंदु से गुजरने वाली रेखा का समीकरण (Equation of a line pssing through intersection point)

एक रेखा जो $a_1x + b_1y + c_1$ = 0 और $a_2x + b_2y + c_2$ = 0 रेखाओं के प्रतिच्छेदन बिंदु से होकर गुजरती है, को निम्नलिखित समीकरण द्वारा दर्शाया जा सकता है:

$(a_1x + b_1y + c_1) + λ (a_2x + b_2y + c_2$) = 0, जहां λ एक अचर है।

नोट

दो रेखाओं का प्रतिच्छेदन बिंदु (Point of intersection of two lines)

यदि हमारे पास दो रेखाएं $a_1x + b_1y + c_1$ = 0 और $a_2x + b_2y + c_2$ = 0 हैं, तो:

$\frac{x}{b_1 c_2 – b_2 c_1} = \frac{y}{c_1 a_2 – c_2 a_1} = \frac{1}{a_1 b_2 – a_2 b_1}$

इस प्रकार, इन दो रेखाओं का प्रतिच्छेदन बिंदु = $\frac{b_1 c_2 – b_2 c_1}{a_1 b_2 – a_2 b_1}, \frac{c_1 a_2 – c_2 a_1}{a_1 b_2 – a_2 b_1}$
जहां $a_1 b_2 – a_2 b_1$ ≠ 0

कोण द्विभाजक के समीकरण (Equations of Angle Bisectors)

दो रेखाओं $a_1x + b_1y + c_1$ = 0 और $a_2x + b_2y + c_2$ = 0 के कोण द्विभाजक के समीकरणों को निम्नानुसार दर्शाया जा सकता है:

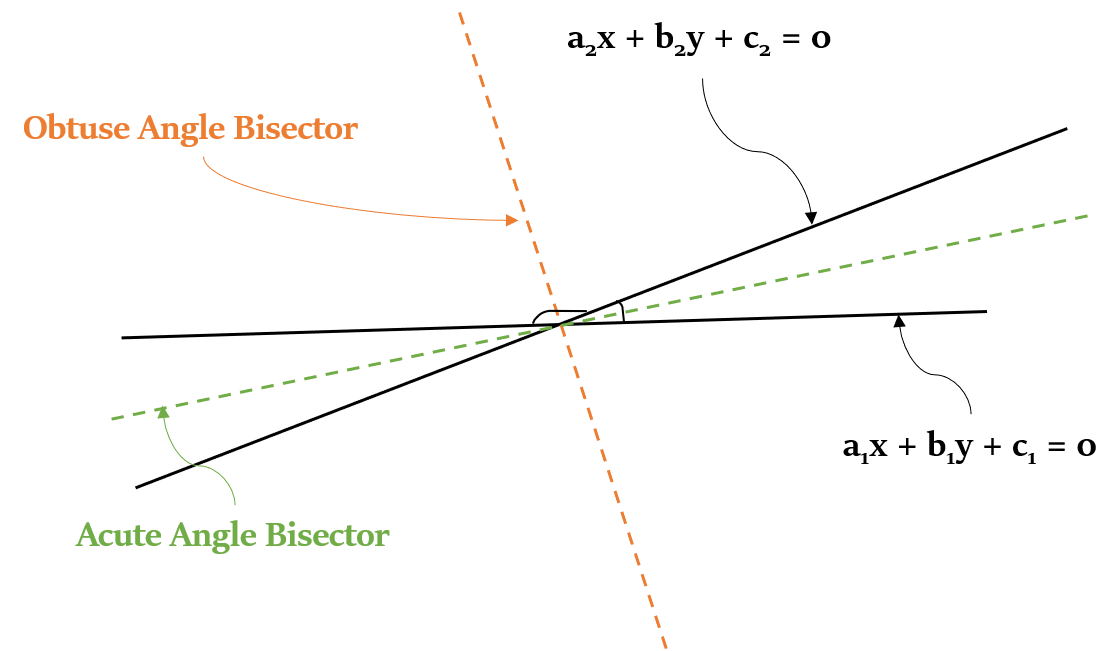
Coordinate Geometry

$\frac{a_1x + b_1y + c_1}{\sqrt{a_1^2 + b_1^2}} = ± \frac{a_2x + b_2y + c_2}{\sqrt{a_2^2 + b_2^2}}$

कैसे निर्धारित करें कि कौन सा द्विभाजक समीकरण न्यून कोण या अधिक कोण का है? (How to determine which bisector equation is of Acute and Obtuse angle?)

अब, आइए देखें कि निम्नलिखित कैसे ज्ञात करें :

• मूल निर्देशांक, रेखाओं के बीच के न्यून कोण (acute angle) या अधिक कोण (obtuse angle) में स्थित है ?
• कौन सा द्विभाजक समीकरण, न्यून कोण समद्विभाजक (acute angle bisector) और अधिक कोण समद्विभाजक (obtuse angle bisector) से मेल खाता है?

चरण I:

सुनिश्चित करें कि $c_1$ और $c_2$ दोनों सकारात्मक हैं। यदि उनमें से एक या दोनों ऋणात्मक हैं, तो संबंधित समीकरण के दोनों पक्षों को -1 से गुणा करके उन्हें धनात्मक बनाएं।

चरण II:

$a_1 a_2 + b_1 b_2$ के चिह्न का पता लगाएं।

अगर $a_1 a_2 + b_1 b_2$ > 0, तो:

"+" चिन्ह अधिक कोण का समद्विभाजक देता है। अर्थात्, अधिक कोण के द्विभाजक का समीकरण होगा: $\frac{a_1x + b_1y + c_1}{\sqrt{a_1^2 + b_1^2}} = \frac{a_2x + b_2y + c_2}{\sqrt{a_2^2 + b_2^2}}$

अगर $a_1 a_2 + b_1 b_2$ < 0, तो:

"+" चिन्ह न्यून कोण का समद्विभाजक देता है। अर्थात्, न्यून कोण के समद्विभाजक का समीकरण होगा: $\frac{a_1x + b_1y + c_1}{\sqrt{a_1^2 + b_1^2}} = \frac{a_2x + b_2y + c_2}{\sqrt{a_2^2 + b_2^2}}$

नोट

दो रेखाओं के बीच का कोण (Angle between two lines)

यदि θ दो रेखाओं y = $m_1x + c_1$ और y = $m_2x + c_2$ के बीच का कोण θ है, तो:
tan θ = $|\frac{m_2 - m_1}{1 + m_2 m_1}|$ या $|\frac{m_1 - m_2}{1 + m_1 m_2}|$

यदि θ दो रेखाओं $a_1x + b_1y + c_1$ = 0 और $a_2x + b_2y + c_2$ = 0 के बीच का कोण है, तो:
tan θ = $\frac{a_2 b_1 – a_1 b_2}{a_1 a_2 + b_1 b_2}$