निर्देशांक ज्यामिति में निर्देशांक और बिंदुओं की स्थिति ढूँढना (Finding Coordinates and Position of points in Coordinate Geometry)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Finding Coordinates and Position of points in Coordinate Geometry, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• निर्देशांक ज्यामिति क्या होती है?
• निर्देशांक ज्यामिति में निर्देशांक और बिंदुओं की स्थिति ढूँढना
• रेखाओं का समीकरण
• निर्देशांक ज्यामिति - दो रेखाएं
• त्रिभुज
• चतुर्भुज
• वृत्त का समीकरण
• बिंदु का प्रतिबिंब

इस लेख में, हम सीखेंगे कि बिंदुओं के मामले में निर्देशांक ज्यामिति की अवधारणाओं का उपयोग कैसे किया जाता है।

एक रेखा के सापेक्ष किसी बिंदु की स्थिति (Position of a point with respect to a line)

हम आसानी से पता लगा सकते हैं कि दिए गए दो बिंदु एक रेखा के एक ही तरफ हैं या विपरीत दिशा में। आइए देखें कैसे।

यदि A ($x_1$, $y_1$) और B ($x_2$, $y_2$) दो बिंदु हैं, और किसी रेखा का समीकरण ax + by + c = 0 है, तो:

वे दो बिंदु रेखा के एक ही तरफ होंगे, यदि: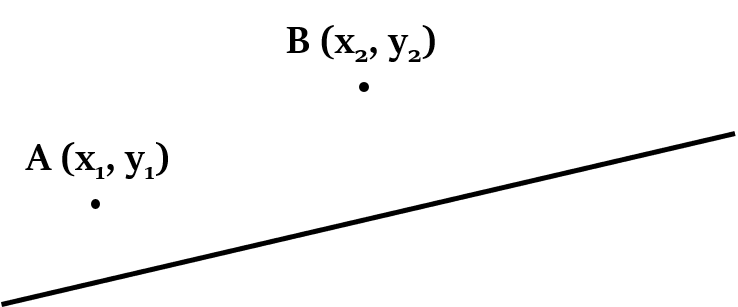

Coordinate Geometry

$(ax_1 + by_1 + c)$ और $(ax_2 + by_2 + c)$ के चिह्न समान हैं।

वे दो बिंदु रेखा के विपरीत दिशा में होंगे (यानि एक बिंदु रेखा के एक तरफ, और दूसरा दूसरी तरफ), यदि: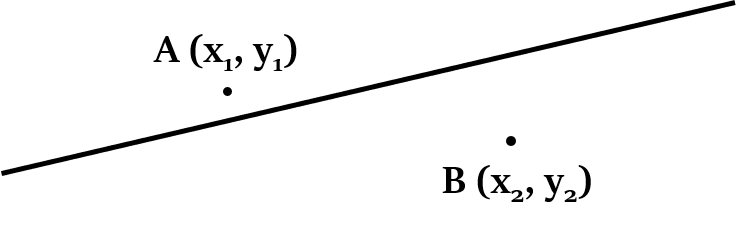

Coordinate Geometry

$(ax_1 + by_1 + c)$ और $(ax_2 + by_2 + c)$ के चिह्न विपरीत हैं।

रेखा को विभाजित करने वाले बिंदु के निर्देशांक ढूँढना (Finding Coordinates of a point dividing a line)

यदि हम उस अनुपात को जानते हैं जिसमें कोई बिंदु किसी रेखा को आंतरिक या बाह्य रूप से विभाजित करता है, तो हम उस बिंदु का निर्देशांक ज्ञात कर सकते हैं।

रेखा खंड का आंतरिक विभाजन (Internal division of a line segment)

यदि कोई बिंदु A (x, y), दो बिंदुओं P ($x_1$, $y_1$) और Q ($x_2$, $y_2$) को मिलाने वाली रेखा को m:n के अनुपात में आंतरिक रूप से विभाजित करता है, तो:

आरेख: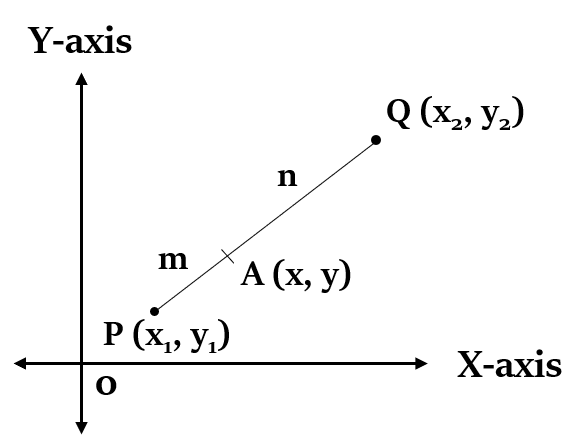

Coordinate Geometry

x = $\frac{m x_2 + n x_1}{m + n}$

y = $\frac{m y_2 + n y_1}{m + n}$

नोट

विशेष मामला

एक रेखाखंड के मध्य-बिंदु के मामले में, m:n = 1:1

तो, दो बिंदुओं P ($x_1$, $y_1$) और Q ($x_2$, $y_2$) को मिलाने वाले रेखा खंड के मध्य-बिंदु के निर्देशांक होंगे:

x = $\frac{x_2 + x_1}{2}$

y = $\frac{y_2 + y_1}{2}$

रेखा खंड का बाहरी विभाजन (External division of a line segment)

यदि कोई बिंदु A (x, y), दो बिंदुओं P ($x_1$, $y_1$) और Q ($x_2$, $y_2$) को मिलाने वाली रेखा को m:n के अनुपात में बाहरी रूप से बाँटता है, तो:

आरेख: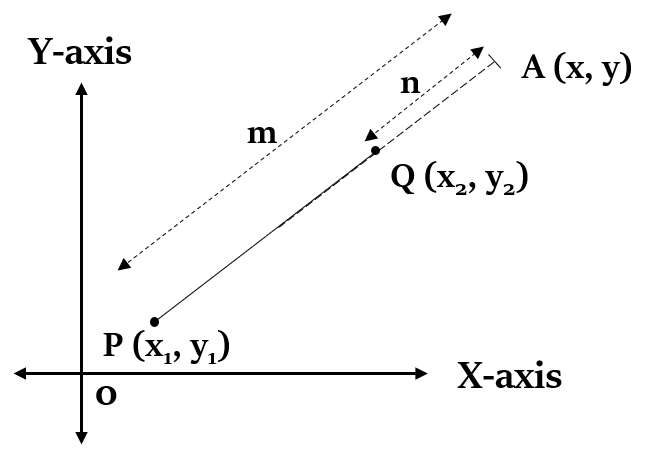

Coordinate Geometry

x = $\frac{m x_2 - n x_1}{m - n}$

y = $\frac{m y_2 - n y_1}{m - n}$

दो निर्देशांकों के बीच की दूरी (Distance between two Coordinates)

यदि हम उनके निर्देशांकों को जानते हैं, तो हम दो बिंदुओं के बीच की दूरी ज्ञात कर सकते हैं।

यदि कार्तीय तल (Cartesian plane) पर हमारे दो बिंदु हैं, P ($x_1$, $y_1$) और Q ($x_2$, $y_2$), तो:

आरेख:

Coordinate Geometry

P और Q के बीच की दूरी, d = $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$

नोट

विशेष मामला

किसी बिंदु P (x, y) और मूल निर्देशांक (0, 0) के बीच की दूरी = $\sqrt{(x - 0)^2 + (y - 0)^2} = \sqrt{x^2 + y^2}$

सीधी रेखा से किसी बिंदु की न्यूनतम दूरी (Minimum distance of a point from a straight line)

एक सीधी रेखा से किसी बिंदु की न्यूनतम दूरी = उस रेखा पर उस बिंदु से गिराए गए लंब की लंबाई।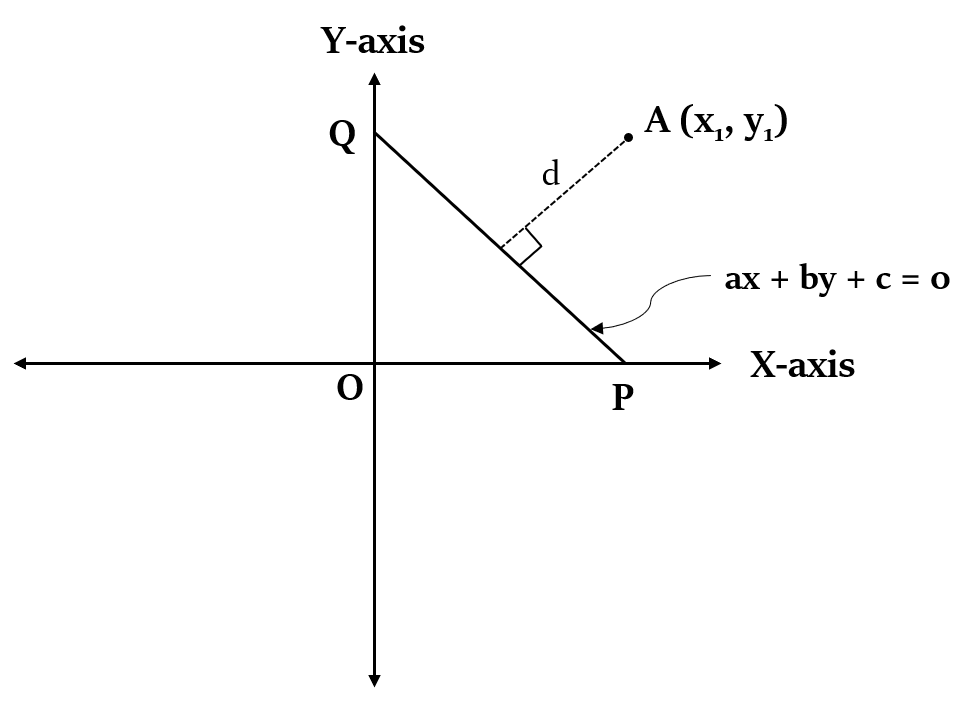

Coordinate Geometry

किसी दिए गए बिंदु ($x_1, y_1$) से एक रेखा ax + by + c = 0 पर लंब (perpendicular) की लंबाई की गणना निम्न सूत्र का उपयोग करके की जा सकती है:

d = $\frac{|a x_1 + b y_1 + c|}{\sqrt{a^2 + b^2}}$

नोट

मूल निर्देशांक (0, 0) से रेखा ax + by + c = 0 पर लंब की लंबाई निम्नलिखित सूत्र द्वारा दी जाती है:

d = $\frac{|c|}{\sqrt{a^2 + b^2}}$

समरेख बिंदु ज्ञात करना (Finding Collinear points)

तीन दिए गए बिंदु (जैसे A, B और C) संरेख हैं (अर्थात वे एक ही सीधी रेखा पर स्थित हैं), यदि निम्नलिखित में से कोई भी शर्त पूरी होती है:

• ∆ABC का क्षेत्रफल शून्य है।
• किन्हीं दो बिंदुओं को मिलाने वाली रेखाओं का ढाल (Slope) समान है। अर्थात् AB का ढाल = BC का ढाल = CA का ढाल।
• यदि किन्हीं दो रेखाखंडों की लंबाइयों का योग तीसरी रेखाखंड के बराबर है। मान लीजिए, यदि AB + BC = AC