त्रिकोणमिति क्या है? (What is Trigonometry?)
Overview
इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - What is Trigonometry?, in Hindi
 नोट
नोटइस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:
त्रिकोणमिति गणित की एक ऐसी शाखा है, जो त्रिभुजों की भुजाओं और कोणों से जुड़े संबंधों का अध्ययन करती है।
 नोट
नोटतो, आम शब्दों में, हम कह सकते हैं कि त्रिकोणमिति त्रिभुजों (triangles) का अध्ययन है।
'Trigonometry' शब्द को तीन ग्रीक शब्दों को मिलाकर बनाया गया है:
- 'tri' - इसका अर्थ है तीन,
- 'gon' - इसका अर्थ है भुजाएँ और
- 'metron' - इसका अर्थ है माप
त्रिकोणमिति के फलन (Functions in trigonometry)
त्रिकोणमिति में फलन मूल रूप से एक समकोण त्रिभुज (right-angled triangle) की भुजाओं के अनुपात होते हैं। वे एक समकोण त्रिभुज के न्यून कोण (acute angle) और उसकी भुजाओं की लंबाई के बीच संबंध को व्यक्त करते हैं।
समकोण त्रिभुज की निम्नलिखित आकृति पर एक नज़र डालें।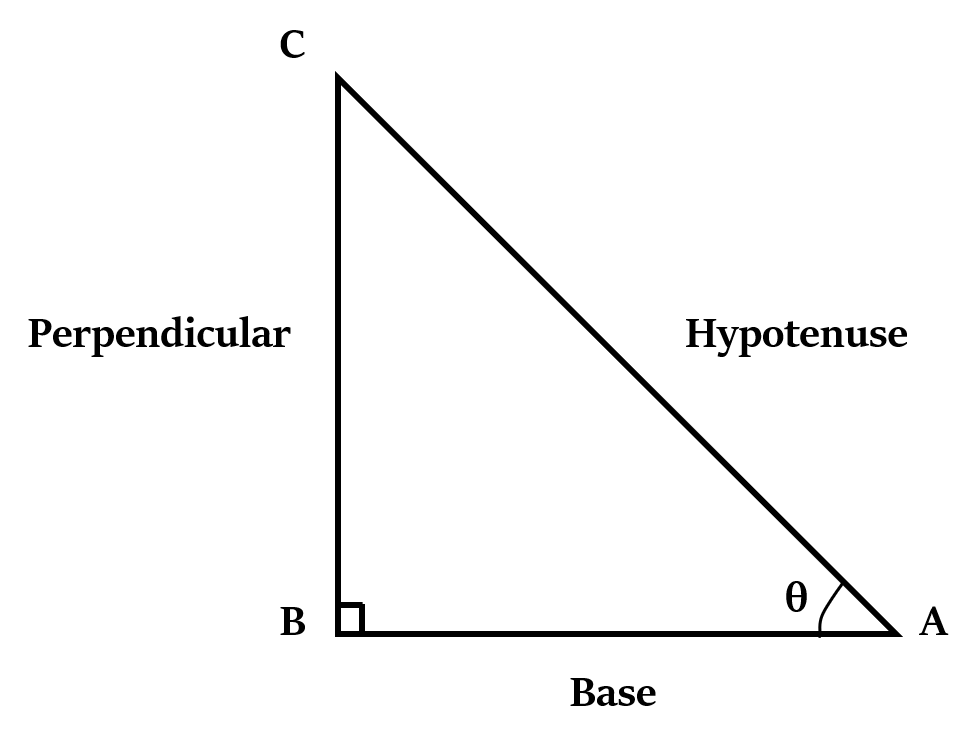
Trigonometry
त्रिकोणमिति में मुख्य फलन निम्नलिखित हैं:
| नाम | त्रिकोणमिति फलन (Trigonometry function) |
|---|---|
| Sine | sin θ = |
| Cosine | cos θ = |
| Tangent | tan θ = |
| Cosecant | cosec θ = |
| Secant | sec θ = |
| Cotangent | cot θ = |
 नोट
नोटSine, Cosine, Tangent, Cosecant, Secant और Cotangent को अक्सर संक्षिप्त रूप में क्रमशः sin, cos, tan, cosec, sec, और cot लिखा जाता है|
 नोट
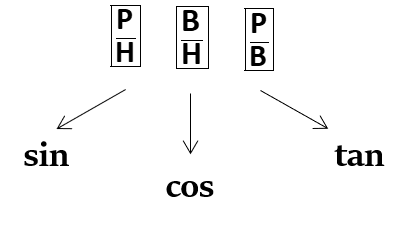
नोटइन अनुपातों को याद रखने के लिए, हम उन्हें एक स्मृतिचिह्न (mnemonic) का उपयोग करके याद कर सकते हैं:
Trigonometry
P → लम्ब (Perpendicular); B → आधार (Base); H → कर्ण (Hypotenuse)त्रिकोणमितीय फलनों के मान (Values of Trigonometric Functions)
आइये, 0° से 90° तक के कुछ महत्वपूर्ण कोणों के लिए त्रिकोणमितीय फलनों के मानों पर एक नज़र डालें।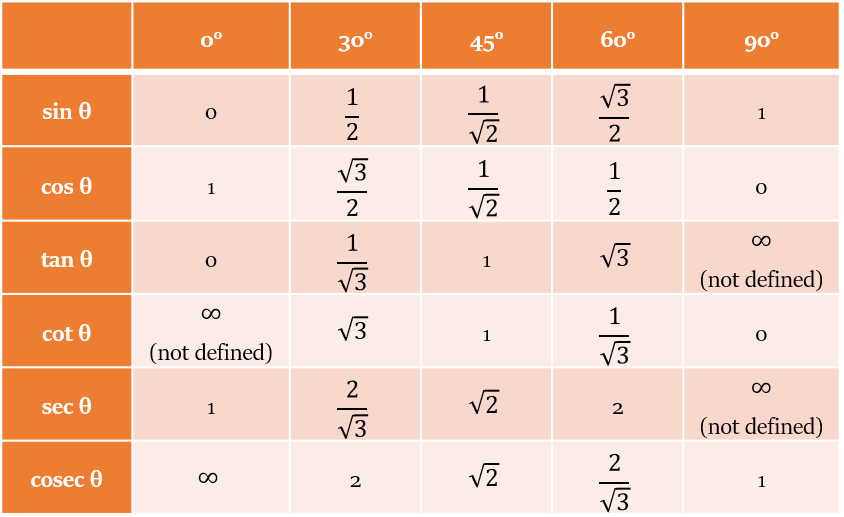
Trigonometry
 नोट
नोटआपको इन मूल्यों को याद रखना चाहिए।
बस sin और cos के मूल्यों को याद रखें, और शायद tan के मूल्यों को भी। यद्यपि आप sin मानों को संगत cos मानों से विभाजित करके tan मान ज्ञात कर सकते हैं।
cosec, sec और cot के मान क्रमशः sin, cos और tan के मानों के व्युत्क्रम (reciprocal) होते हैं।
 नोट
नोट= ∞; = -∞
इन दोनों को परिभाषित नहीं किया गया है।
त्रिकोणमितीय फलनों के चिन्ह (Signs of Trigonometric Functions)
तो, अब हम 30°, 45°, 90° आदि कोणों के लिए त्रिकोणमितीय फलनों के मान जानते हैं। ये सभी कोण पहले चतुर्थांश (first quadrant) में आते हैं।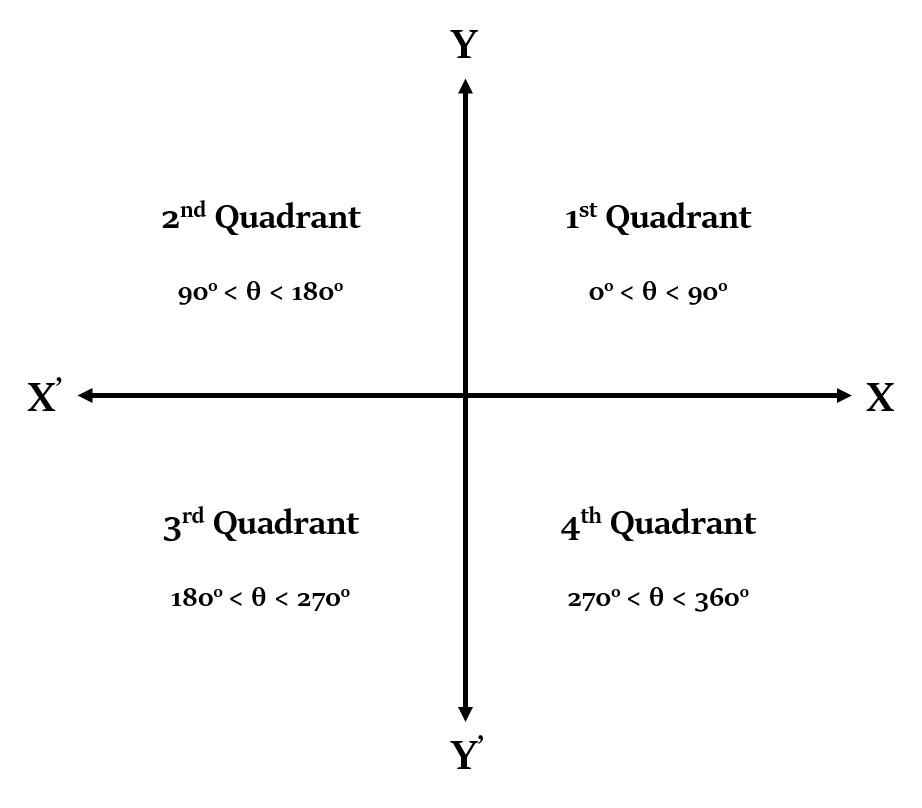
Trigonometry
लेकिन अन्य चतुर्थांशों में ऐसे कोणों का क्या, जैसे की, 120°, 225°, 180° आदि?
यहां तीन चरण दिए गए हैं जिनका आपको पालन करने की आवश्यकता है:
चरण 1: उस चतुर्थांश का पता लगाएं, जिसमें वो कोण हैं।
चरण 2: संबंधित त्रिकोणमितीय फलन का मान ज्ञात करने के लिए उपयुक्त सूत्र का प्रयोग करें।
चरण 3: उपयुक्त चिन्ह का प्रयोग करना न भूलें।
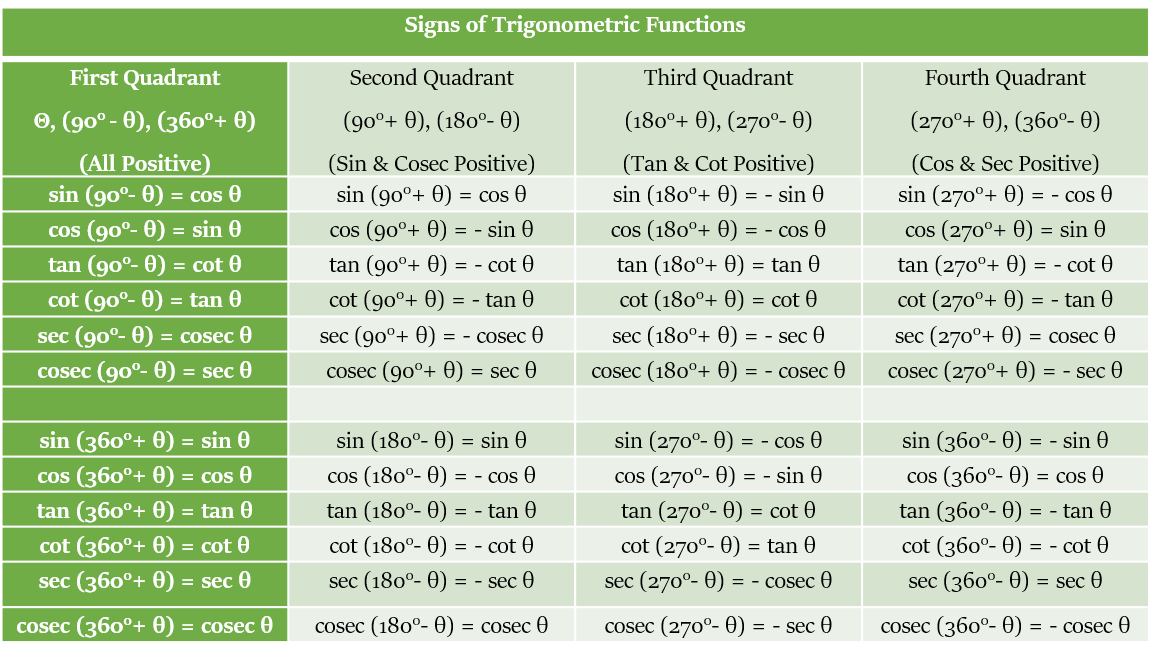
Trigonometry
हम उपरोक्त तालिका से निम्नलिखित निष्कर्ष निकाल सकते हैं:
त्रिकोणमितीय फलन का चिन्ह इस बात पर निर्भर करेगा कि कोण किस चतुर्थांश में आता है। इसे निम्नलिखित आकृति का उपयोग करके दर्शाया जा सकता है:
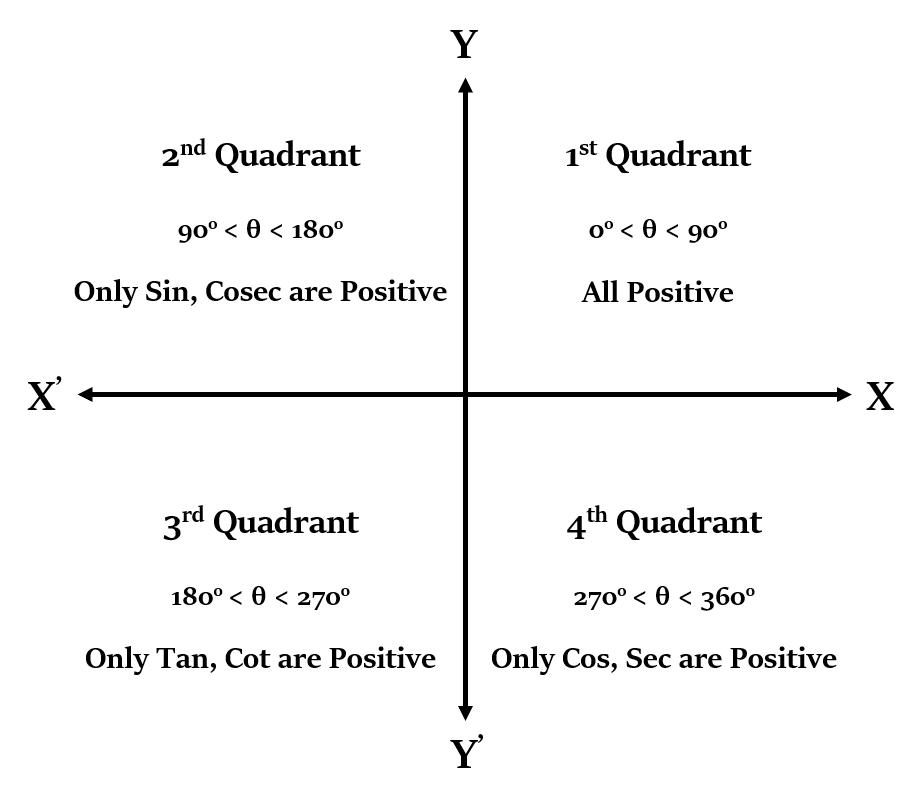
Trigonometry
जब कोण 180° का गुणज हो, उदा. 0°, 180°, 360°,... इत्यादि, तो त्रिकोणमितीय फलन परिवर्तित नहीं होगा। उदाहरण के लिए, sin (180° - θ) = sin θ, tan (180° + θ) = tan θ, आदि।
जब कोण 90° का विषम गुणज हो, उदा. 90°, 270°,... इत्यादि, तो त्रिकोणमितीय फलन बदल जाएगा। उदाहरण के लिए, cos (90° - θ) = sin θ, sin (270° - θ) = - cos θ
 नोट
नोटइसके अलावा, ध्यान दें कि:
Trigonometry
डिग्री और रेडियन के बीच संबंध (Relation between Degree and Radian)
1 radian =
और 1° = radian
उदाहरण के लिए, 90° = 90° × radian
 नोट
नोट180° को π के रूप में भी लिखा जा सकता है
360° को 2π के रूप में भी लिखा जा सकता है
नीचे दिखाए गए आरेख पर एक नज़र डालें:
Trigonometry
किसी वृत्त में, वृत्त के केंद्र पर एक चाप द्वारा बनाए गए कोण का रेडियन, चाप (arc) की लंबाई और वृत्त की त्रिज्या (radius) का अनुपात होता है।
दूसरे शब्दों में, त्रिज्या के बराबर लंबाई का एक चाप, वृत्त के केंद्र पर 1 रेडियन का कोण बनाएगा।
Trigonometry

