अनुपात की मूल अवधारणाएँ (Basic Concepts of Ratio)

Overview

इस लेख में हम क्वांटिटेटिव एप्टीटुड (गणित) के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Basic Concepts of Ratio, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• Proportion
• Partnership

दो डेटा मानों की तुलना कैसे करें? (How to compare two data values?)

यदि हम दो संख्याओं की तुलना करना चाहते हैं, तो हमारे पास कौन से उपकरण या विधियाँ उपलब्ध हैं?

आइए इसे एक उदाहरण से समझने की कोशिश करते हैं।

एक जूते की कीमत रु. 2500 और एक मोबाइल की कीमत रु. 5000 है|

एक ही प्रकार के दो डेटा मानों की तुलना, हम तीन विधियों का उपयोग करके कर सकते हैं:

• अंतर विधि, (a - b):
  अंतर = रु. 2500

• प्रतिशत विधि:
  

मोबाइल की कीमत के प्रतिशत के रूप में जूते की कीमत = ($\frac{2500}{5000}$) × 100 = 50%

• विभाजन या अनुपात विधि, (a/b या a:b):
  

इन दो मानों का अनुपात = $\frac{2500}{5000} = \frac{1}{2}$

जबकि अंतर विधि को समझना बहुत आसान है, हम प्रतिशत विधि का अध्ययन एक दुसरे लेख में कर चुके हैं। इस लेख में हमारा ध्यान, अनुपात पर होगा।

अनुपात क्या है? (Ratio kya hota hai?)

अनुपात - यह एक मात्रा की उसी प्रकार की दूसरी मात्रा से तुलना करने का एक तरीका है।

इसे : चिन्ह द्वारा दर्शाया जाता है, जैसे की a:b

अनुपात को भिन्नात्मक रूप में भी लिखा जा सकता है, जैसे की a:b = a/b

उदाहरण के लिए:
रु. 15 और रु. 25 का अनुपात = 15/25 = 3/5, यानी 3:5
10 मिनट और 1 घंटे का अनुपात = 10/60 = 1/6, यानी 1:6

अनुपात की मूल अवधारणाएँ (Basic Concepts of Ratio)

अवधारणा 1: सापेक्ष मूल्य (Relative values)

अनुपात केवल सापेक्ष मूल्यों का अनुमान देते हैं, वास्तविक परिमाण (magnitude) का नहीं।

उदाहरण के लिए:
यदि एक कक्षा में लड़के और लड़कियों का अनुपात 3 : 5 है, तो इसका सीधा सा अर्थ है कि:
लड़कों की संख्या / लड़कियों की संख्या = 3/5

इसका मतलब यह नहीं है कि कक्षा में 3 लड़के और 5 लड़कियां हैं। हम निश्चित रूप से कक्षा में लड़के और लड़कियों की असली संख्या नहीं बता सकते।

जैसे की, निम्नलिखित सभी मामलों पर एक नज़र डालें, जिन सबमें लड़कों और लड़कियों का अनुपात 3:5 ही है।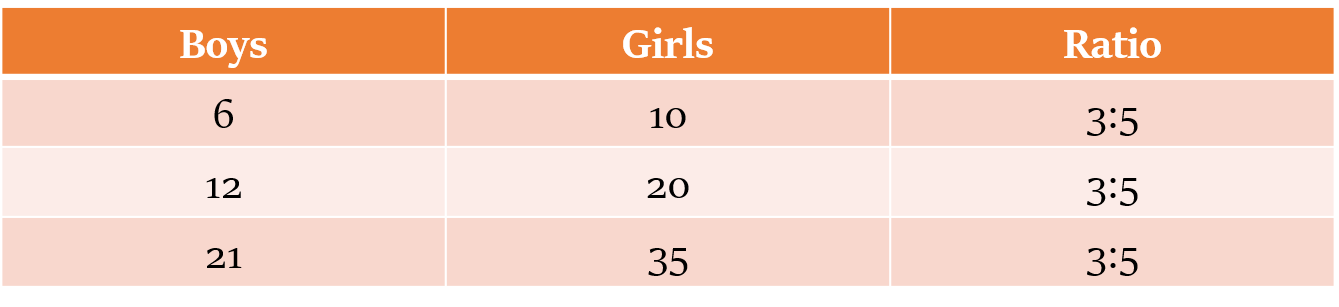

ratio

अवधारणा 2: सामान्य कारकों को हटा दें (Remove common factors)

संख्याओं का अनुपात किसी भी समान कारकों को हटाने के बाद ही व्यक्त किया जाता है, अर्थार्थ जो अनुपात के सभी पदों में होते हैं।

उदाहरण के लिए, यदि दो मात्राएँ 6 और 9 हैं:
6 : 9 = 2 : 3
(उनके बीच समान कारक 3 को निकालने के बाद)

यदि तीन मात्राएँ 6, 14 और 18 हैं:
6 : 14 : 18 = 3 : 7 : 9
(उनके बीच समान कारक 2 को निकालने के बाद)

अवधारणा 3

अगर, A : B : C = 1/3 : 1/5 : 1/7
तो, A : B : C = 35 : 21 : 15
(हमने LCM 105 से गुणा किया है)

लेकिन अगर, A/3 = B/5 = C/7
तो, A : B : C = 3 : 5 : 7

अवधारणा 4: अनुपात से असल मात्राएँ ज्ञात करना (Finding original quantities from a ratio)

मान लीजिए कि दो राशियाँ हैं (जिनके मूल या असल मान क्रमशः A और B हैं), और वो a : b के अनुपात में हैं।

हम जानते हैं कि अनुपात a : b प्राप्त करने के लिए A और B से कोई समान कारक k (>0) हटा दिया गया होगा। इसलिए, हम दो राशियों के मूल मान इस प्रकार लिख सकते हैं:
A = ak और
B = bk

उदाहरण के लिए, यदि दो व्यक्तियों के अंक 5 : 3 के अनुपात में हैं, तो हम उनके व्यक्तिगत अंकों को क्रमशः 5k और 3k लिख सकते हैं।

आइए एक और उदाहरण पर विचार करें:
यदि यह दिया जाता है, कि एक कक्षा में लड़के और लड़कियों का अनुपात 3 : 5 है
इससे हम केवल एक ही जानकारी इकट्ठा कर सकते हैं - अगर 3k लड़के हैं, तो 5k लड़कियां होंगी।
अब यदि कोई और डेटा दिया जाता है जिससे हम k का मान ज्ञात कर पाएं, तो हम कक्षा में लड़कों और लड़कियों की सही संख्या का पता लगा सकते हैं।
उदाहरण के लिए, यदि यह दिया जाता है कि अगर लड़कों की संख्या के दुगने से लड़कियों की संख्या को घटा दिया जाये, तो 10 प्राप्त होता है। तो हम यह समीकरण बना सकते हैं: 6k - 5k = 10, जो हमें k = 10 देता है। अतः, कक्षा में 30 लड़के और 50 लड़कियां होंगी।

प्र. एक पार्किंग स्थल में कार और बाइक का अनुपात 7:11 है। कारों की संख्या से 56 अधिक बाइक खड़ी हैं। पार्किंग में खड़ी कारों की संख्या कितनी है?

(a) 91   (b) 98    (c) 147   (d) 154

व्याख्या :
1 2

प्र. एक खेत में गायों और सूअरों का अनुपात 1:3 था। 50 और गायों को खेत में लाए जाने के बाद, गायों और सूअरों का अनुपात 1:1 हो गया। अब खेत में गायों की कुल संख्या कितनी है?

(a) 75   (b) 100    (c) 41250   (d) निर्धारित नहीं किया जा सकता

व्याख्या :
1 2

अवधारणा 5

यदि दो राशियाँ a : b के अनुपात में हों, और उन दो राशियों का योग S हो, तो

पहली राशि = $\frac{a}{(a + b)}$ × S

दूसरी राशि = $\frac{b}{(a + b)}$ × S

प्र. दो संख्याओं का योग 42 है। यदि यह दो संख्याएँ 4:3 के अनुपात में हैं, तो छोटी संख्या ज्ञात कीजिए।

व्याख्या :
1 2

अनुपात के प्रकार (Types of Ratios)

बड़ी संख्या का छोटी संख्या से अनुपात (Ratio of greater inequality)

अनुपात a : b, जहां a > b हो (उदाहरण के लिए, 5 : 4)

छोटी संख्या का बड़ी संख्या से अनुपात (Ratio of lesser inequality)

अनुपात a : b, जहां a < b हो (उदाहरण के लिए, 4: 5)

समान संख्याओं का अनुपात (Ratio of equality)

अनुपात a : b, जहां a = b हो (उदाहरण के लिए, 1 : 1)

कुछ अन्य प्रकार के अनुपात (Some other kinds of ratios)

• a और b का डुप्लिकेट अनुपात (Duplicate ratio) = $a^2 : b^2$

• a और b का ट्रिप्लीकेट अनुपात (Triplicate ratio) = $a^3 : b^3$

• a और b का सब-डुप्लिकेट अनुपात (Sub duplicate ratio) = √a : √b

• a और b का सब-ट्रिप्लीकेट अनुपात (Sub triplicate ratio) = $(𝑎)^{1/3} : (b)^{1/3}$

• a : b, c : d, e : f का मिश्र अनुपात (Compound ratio) = $\frac{ace}{bdf}$

अनुपात के गुण (Properties of Ratios)

गुण 1: गुणा/भाग

अनुपात समान रहता है यदि अंश (numerator) और हर (denominator) दोनों को एक ही गैर-शून्य संख्या से गुणा या विभाजित किया जाता है।

$\frac{a}{b} = \frac{pa}{pb} = \frac{qa}{qb}$ (जहाँ p, q ≠ 0)

$\frac{a}{b} = \frac{\frac{a}{p}}{\frac{b}{p}} = \frac{\frac{a}{q}}{\frac{b}{q}}$ (जहाँ p, q ≠ 0)

उदाहरण के लिए: 5/1 = 10/2 = 15/3 = 50/10 आदि।

गुण 2: योग

जब हम अनुपात के दोनों पदों में समान मात्रा x (धनात्मक) जोड़ते हैं, तो हमें निम्नलिखित परिणाम प्राप्त होते हैं:

यदि a > b, तो (a + x) : (b + x) < a : b
उदाहरण के लिए, अगर a/b = 11/10 = 1.1, तो फिर दोनों में 90 जोड़ने पर हमें 101/100 = 1.01 मिलता है
(मान 1 के करीब आता रहता है, क्योंकि हम दोनों में घनात्मक मान जोड़ रहे हैं)

यदि a < b, तो (a + x) : (b + x) > a : b
उदाहरण के लिए, अगर a/b = 9/10 = 0.90, तो फिर दोनों में 90 जोड़ने पर हमें 99/100 = 0.99 मिलता है
(मान 1 के करीब आता रहता है, क्योंकि हम दोनों में घनात्मक मान जोड़ रहे हैं)

यदि a = b, तो (a + x) : (b + x) = a : b = 1 : 1

प्र. दो संख्याएँ 4:5 के अनुपात में हैं। यदि प्रत्येक में 7 जोड़ दिया जाए, तो दोनों संख्याओं का अनुपात 5:6 हो जाता है। बड़ी संख्या ज्ञात कीजिए।

व्याख्या :
1 2