क्षेत्रमिति - पिरामिड (Mensuration - Pyramid)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Pyramid, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• क्षेत्रमिति क्या होती है?
• क्षेत्रमिति - घन और घनाभ
• क्षेत्रमिति - गोला
• क्षेत्रमिति - बेलन
• क्षेत्रमिति - शंकु
• क्षेत्रमिति - प्रिज्म
• क्षेत्रमिति - पिरामिड

इस लेख में, हम क्षेत्रमिति के एक महत्वपूर्ण विषय, पिरामिड (शुंडाकार स्तंभ) से संबंधित अवधारणाओं और सूत्रों के बारे में जानने जा रहे हैं।

पिरामिड क्या होता है? (What is a Pyramid?)

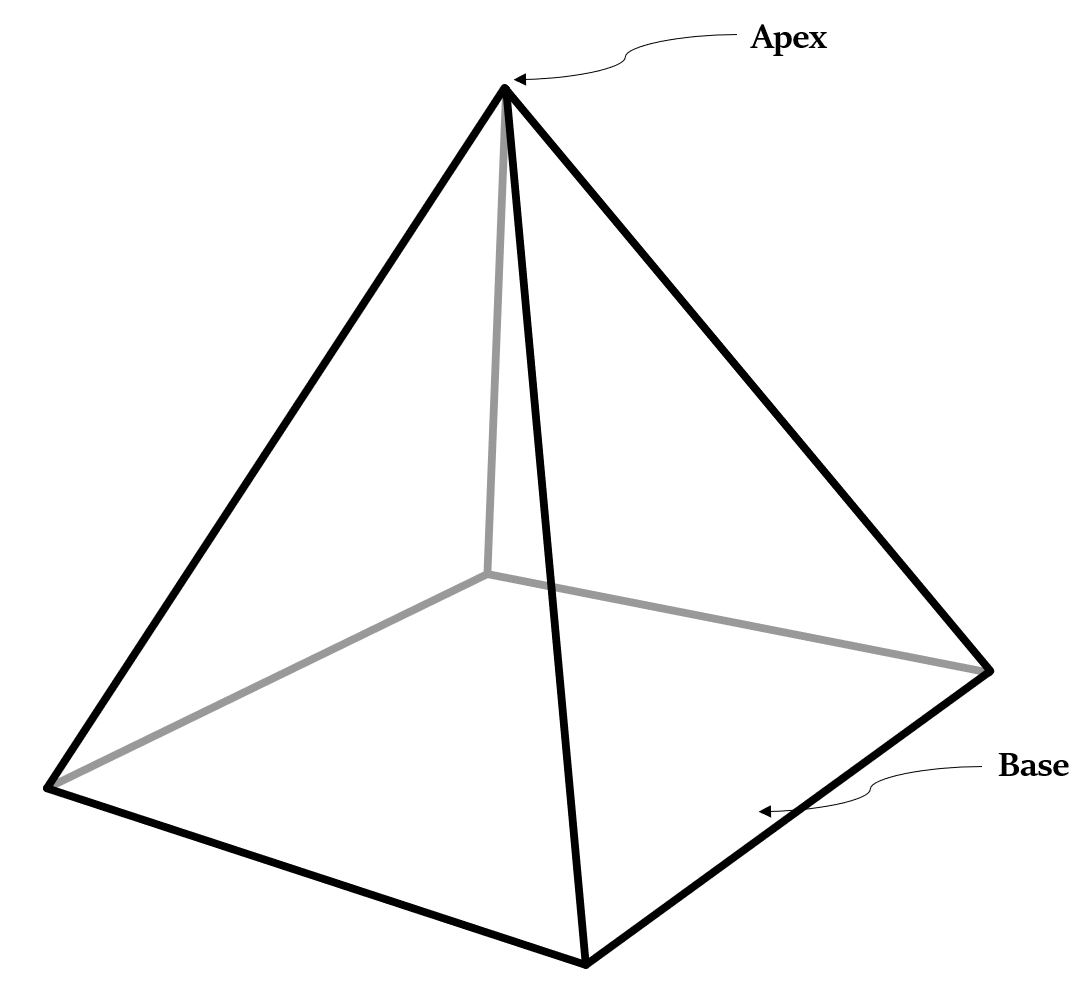
पिरामिड एक त्रिविमीय बहुफलक (polyhedron) है, जिसमें:

• आधार एक बहुभुज होता है (उनकी भुजाएं कितनी भी हो सकती हैं), और
• अन्य फलक एक उभयनिष्ठ शीर्ष (vertex) वाले त्रिभुज होते हैं|
  

  Mensuration

नोट

पिरामिड का शीर्ष (Apex of a Pyramid) - यह एक ऐसा बिंदु है जहाँ पिरामिड के सभी त्रिभुजाकार फलक मिलते हैं।

n-पक्षीय आधार (n-sided base) वाले पिरामिड में n + 1 शीर्ष (vertices), n + 1 फलक (faces) और 2n किनारे (edges) होते हैं।
उदाहरण के लिए, उपरोक्त आकृति में आधार की 4 भुजाएँ हैं, और इसलिए पिरामिड में 5 शीर्ष, 5 फलक और 8 किनारे हैं।

लम्ब पिरामिड (Right Pyramid): यह एक ऐसा पिरामिड है जिसकी धुरी इसके आधार के लंबवत होती है।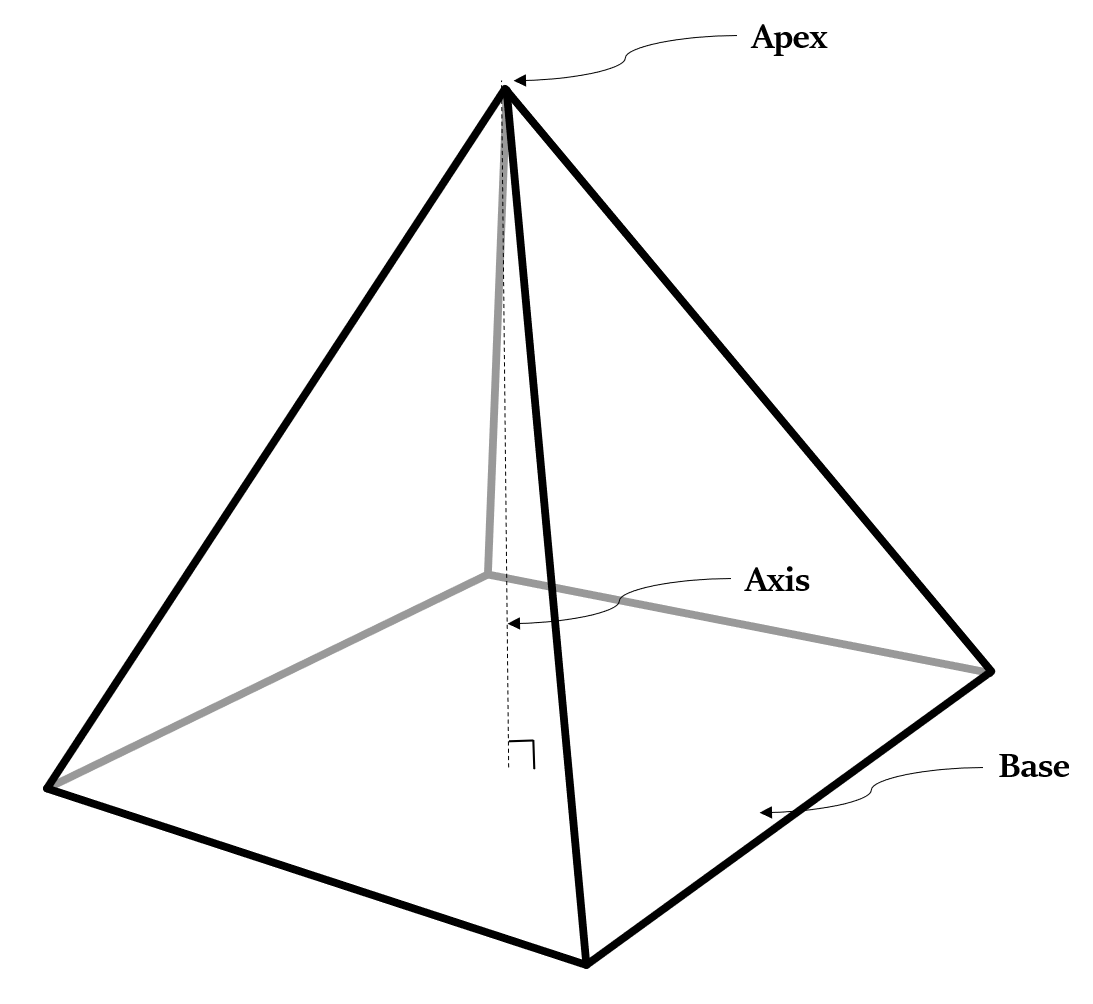

Mensuration

समभुज आधार पिरामिड (नियमित पिरामिड, Regular Pyramid): यह एक ऐसा पिरामिड है जिसका आधार एक नियमित आकृति (regular figure) है, अर्थात इसके आधार की सभी भुजाएँ समान हैं।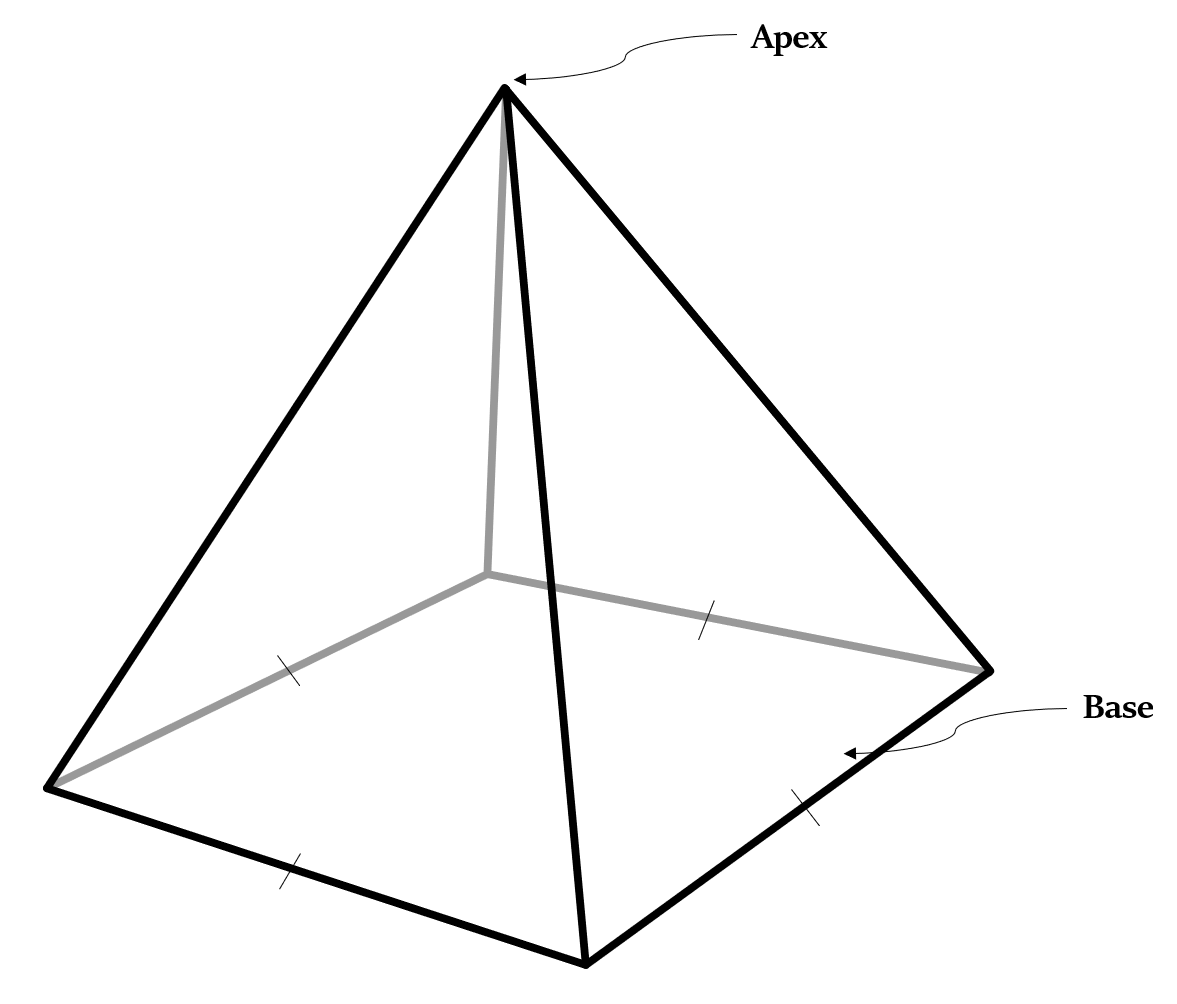

Mensuration

नोट

छिन्नक (frustum) एक 3-D ठोस आकृति का वह भाग है, जो इसे काटने वाले एक या दो समानांतर तलों के बीच स्थित होता है।

उदाहरण के लिए, शंकु का छिन्नक, पिरामिड का छिन्नक, आदि।

एक पिरामिड का छिन्नक (frustum of a pyramid) प्राप्त करने के लिए, हम इसे इसके आधार के समानांतर एक समतल द्वारा काटते हैं। इस तल और मूल पिरामिड के आधार के बीच ठोस का भाग पिरामिड के छिन्नक के रूप में जाना जाता है।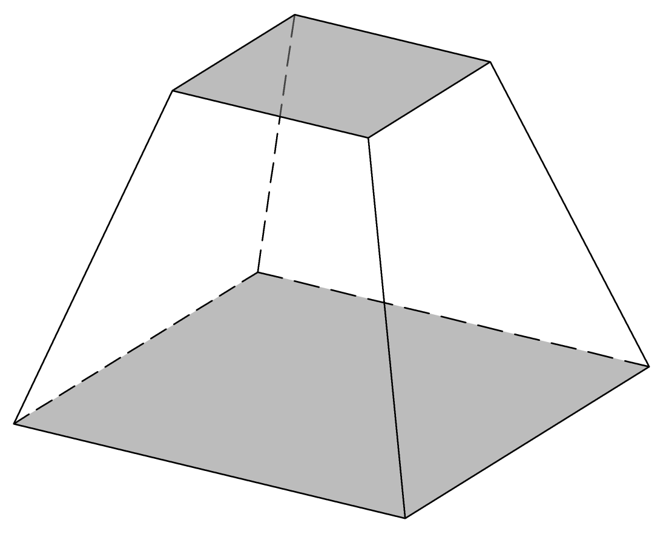

Mensuration

पिरामिड से संबंधित सूत्र (Formulae related to Pyramids)

सूत्र 1: तिरछी ऊंचाई (या ढलान की ऊंचाई, Slant Height)

एक नियमित लम्ब-पिरामिड (regular right-pyramid) की तिरछी ऊँचाई (slant height) वह रेखा-खंड है, जो आधार की किसी भी भुजा के मध्य-बिंदु को शीर्ष (vertex) से जोड़ती है।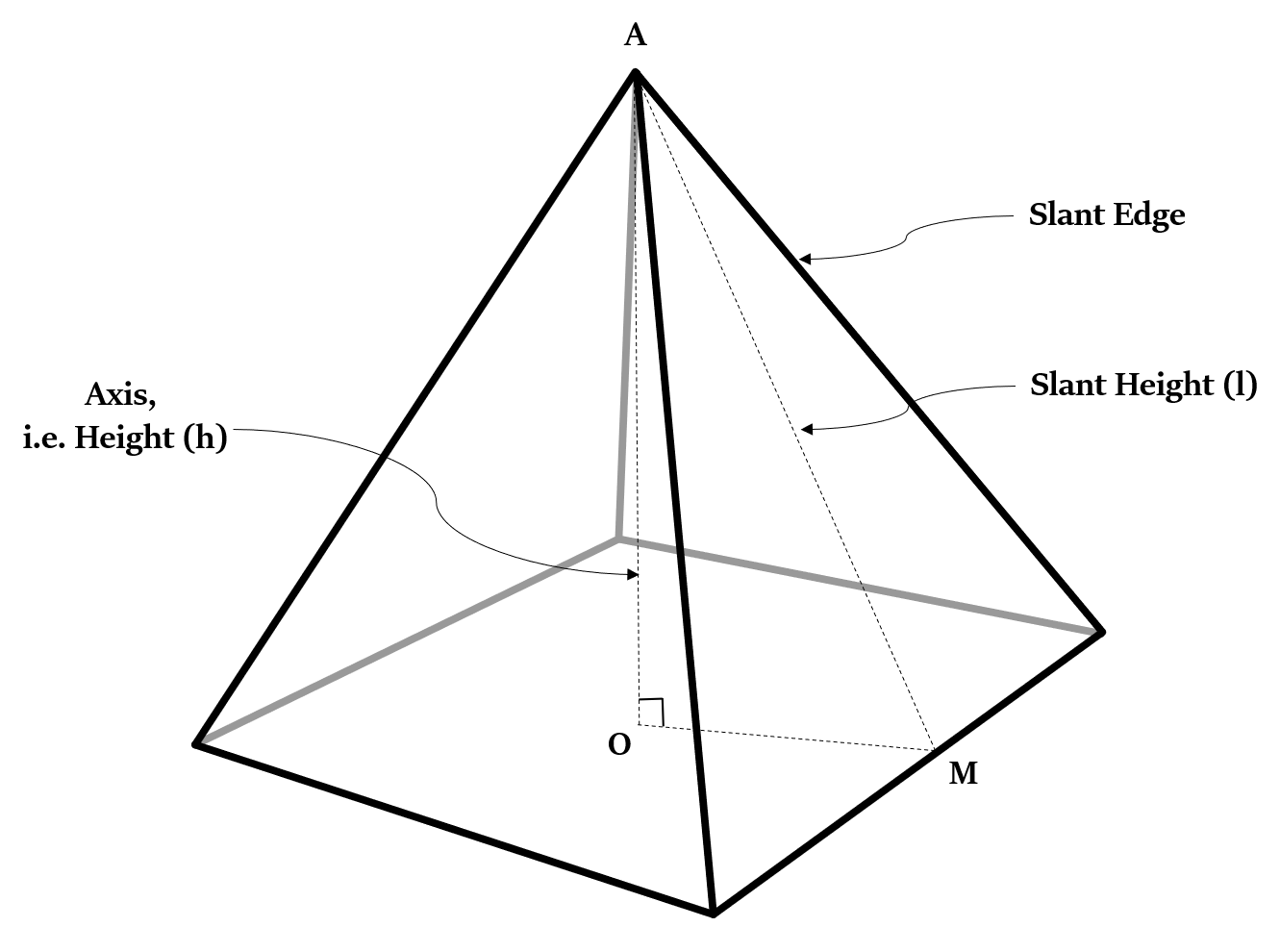

Mensuration

उपरोक्त आकृति में, O आधार का केंद्र है और AM तिरछी ऊंचाई है।
साथ ही, चूंकि ∆AOM एक समकोण त्रिभुज (right-angled triangle) है, इसलिए पाइथागोरस प्रमेय द्वारा:
$AM^2 = AO^2 + OM^2$

सूत्र 2: आयतन (Volume)

पिरामिड का आयतन = $\frac{1}{3}$ × आधार क्षेत्र × ऊँचाई

सूत्र 3: पृष्ठीय क्षेत्रफल (Surface Area)

पार्श्व पृष्ठीय क्षेत्र (Lateral surface area) = $\frac{1}{2}$ × आधार की परिधि (Perimeter) × तिरछी ऊंचाई (Slant height)

कुल पृष्ठीय क्षेत्रफल (Total surface area) = पार्श्व पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल

आधार के अनुसार पिरामिड के प्रकार (Types of Pyramids as per their Base)

हम पहले से ही जानते हैं कि पिरामिड का आधार कितनी भी भुजाओं वाला बहुभुज (polygon) हो सकता है।

अतः आधार के प्रकार के आधार पर हमें विभिन्न प्रकार के पिरामिड मिलते हैं।

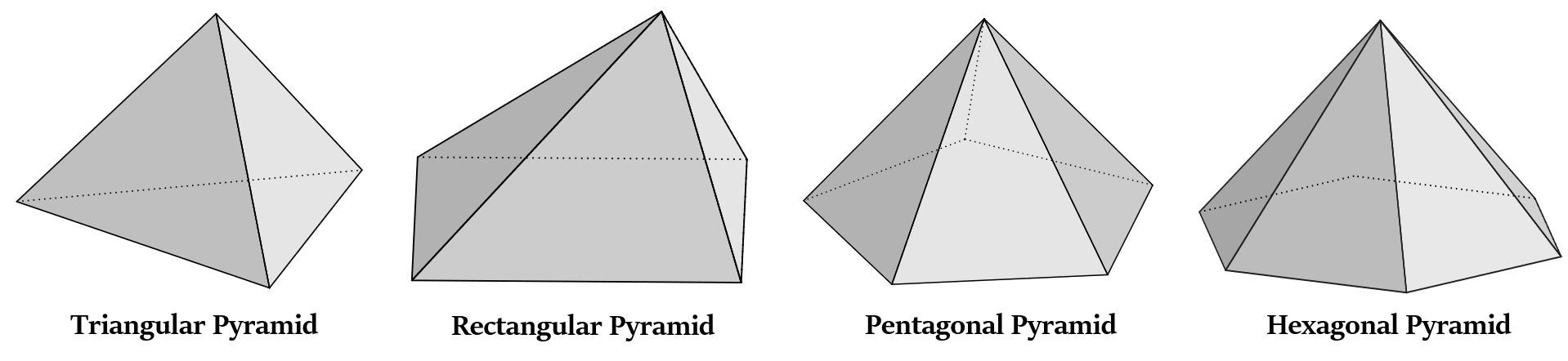
• त्रिकोणीय पिरामिड (Triangular pyramid, Tetrahedron) - इसका 3 भुजाओं वाला त्रिकोणीय आधार होता है।
• आयताकार या वर्गाकार पिरामिड (Rectangular or Square pyramid) - इसका 4 भुजाओं वाला वर्गाकार/आयताकार आधार होता है।
• पंचकोणीय पिरामिड (Pentagonal pyramid) - इसका 5 भुजाओं वाला पंचकोणीय आधार होता है।
• षट्कोणीय पिरामिड (Hexagonal pyramid) - इसका 6 भुजाओं वाला षट्कोणीय आधार होता है।
• और इसी तरह आगे भी .....
  

  Mensuration

हम इनमें से कुछ पिरामिडों का आगे अधिक विस्तार से अध्ययन करेंगे।

चतुष्फलक क्या होता है? (What is a Tetrahedron?)

एक चतुष्फलक (या tetrahedron, चतुर्पाश्वीय) एक त्रिभुजाकार पिरामिड (triangular pyramid) होता है, अर्थात इसके सभी फलक त्रिभुज होते हैं, जिसमें आधार बहुभुज भी शामिल है।

चतुष्फलक के प्रकार (Types of Tetrahedrons)

चतुष्फलकों को विभिन्न मापदंडों के आधार पर वर्गीकृत किया जा सकता है।

फलकों के आधार पर वर्गीकरण (Classification based on Faces)

• समचतुष्फलक (नियमित चतुष्फलक, Regular Tetrahedron) - यदि चतुष्फलक के चारों फलक समबाहु त्रिभुज (equilateral triangles) हैं।

• अनियमित चतुष्फलक (Irregular Tetrahedron) - ये चतुष्फलक वो हैं, जो नियमित चतुष्फलक नहीं हैं।

नोट

सम-त्रिकोणीय चतुष्फलक (Equi-triangular Tetrahedron) - यदि चतुष्फलक का आधार एक समबाहु त्रिभुज (equilateral triangle) है, और अन्य त्रिकोणीय फलक सर्वांगसम (बिल्कुल समान, congruent) समद्विबाहु त्रिभुज (isosceles triangles) हैं। यह एक प्रकार का अनियमित चतुष्फलक है।

शीर्ष की स्थिति के आधार पर वर्गीकरण (Classification based on Position of Apex)

• लम्ब चतुष्फलक (Right tetrahedrons) - यदि किसी चतुष्फलक का शीर्ष उसके आधार के केंद्र के ठीक ऊपर है।
  
  एक लम्ब चतुष्फलक नियमित हो सकता है (यदि सभी चेहरे समान हैं) या अनियमित (यदि आधार को छोड़कर, बाकी सभी चेहरे समान हैं)।
  
  कोई भी नियमित चतुष्फलक हमेशा एक लम्ब चतुष्फलक होता है।

• तिरछा चतुष्फलक (Oblique tetrahedrons) - ये चतुष्फलक वो हैं, जो लम्ब चतुष्फलक नहीं हैं।
  
  जैसा कि हम जल्द ही अध्ययन करेंगे, एक तिरछा चतुष्फलक भी एक अनियमित चतुष्फलक ही होता है।

नोट

दरअसल, जब भी हम किसी भी तरह के पिरामिड के सामने लम्ब (right) शब्द का इस्तेमाल करते हैं, तो इसका मतलब है कि उस पिरामिड का शीर्ष सीधे उसके आधार के केंद्र के ऊपर है।

अब, आइए चतुष्फलकों के बारे में अधिक विस्तार से अध्ययन करें।

समचतुष्फलक (Regular Tetrahedron, नियमित चतुष्फलक)

समचतुष्फलक के सभी चार फलक सर्वांगसम समबाहु त्रिभुज (congruent equilateral triangles) होते हैं (इसके आधार सहित).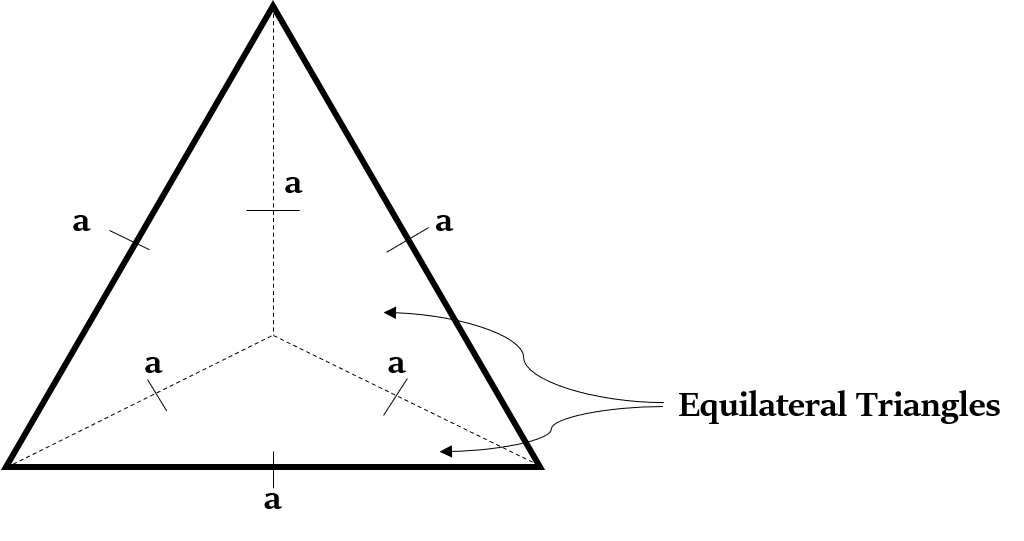

Mensuration

तो, समचतुष्फलक के सभी किनारों (edges) की लंबाई बराबर होती है।

नोट

समचतुष्फलक का शीर्ष (Apex) इसके आधार के केंद्र के ठीक ऊपर होता है। तो, सभी समचतुष्फलक / नियमित चतुष्फलक वास्तव में लम्ब समचतुष्फलक (Right Regular tetrahedrons) होते हैं|

समचतुष्फलक से संबंधित सूत्र (Formulae related to Regular Tetrahedrons)

सूत्र 1: आयतन (Volume)

पिरामिड का आयतन = $\frac{1}{3}$ × आधार क्षेत्र × ऊँचाई

तो, एक लम्ब सम-त्रिकोणीय चतुष्फलक (Right Equi-triangular Tetrahedron) का आयतन = $\frac{1}{3}$ × आधार क्षेत्र × ऊँचाई = $\frac{1}{3} × \frac{\sqrt{3}}{4} a^2 × \frac{\sqrt{2}}{\sqrt{3}}a = \frac{\sqrt{2}}{12} a^3$

सूत्र 2: पृष्ठीय क्षेत्रफल (Surface Area)

पार्श्व पृष्ठीय क्षेत्रफल (Lateral surface area) = तीन सर्वांगसम समबाहु त्रिभुजों (congruent equilateral triangles) के क्षेत्रफलों का योग = 3 × $\frac{\sqrt{3}}{4} a^2$

कुल पृष्ठीय क्षेत्रफल (Total surface area) = चार सर्वांगसम समबाहु त्रिभुजों (congruent equilateral triangles) के क्षेत्रफलों का योग = 4 × $\frac{\sqrt{3}}{4} a^2 = \sqrt{3} a^2$

लम्ब सम-त्रिकोणीय चतुष्फलक (Right Equi-triangular Tetrahedron)

लम्ब सम-त्रिकोणीय चतुष्फलक (Right Equi-triangular Tetrahedron) का आधार एक समबाहु त्रिभुज (equilateral triangle) होता है। इसके शेष फलक सर्वांगसम (बिल्कुल समान) समद्विबाहु त्रिभुज (isosceles triangle) होते हैं। तो, इसका शीर्ष अपने आधार के केंद्र के ठीक ऊपर होता है।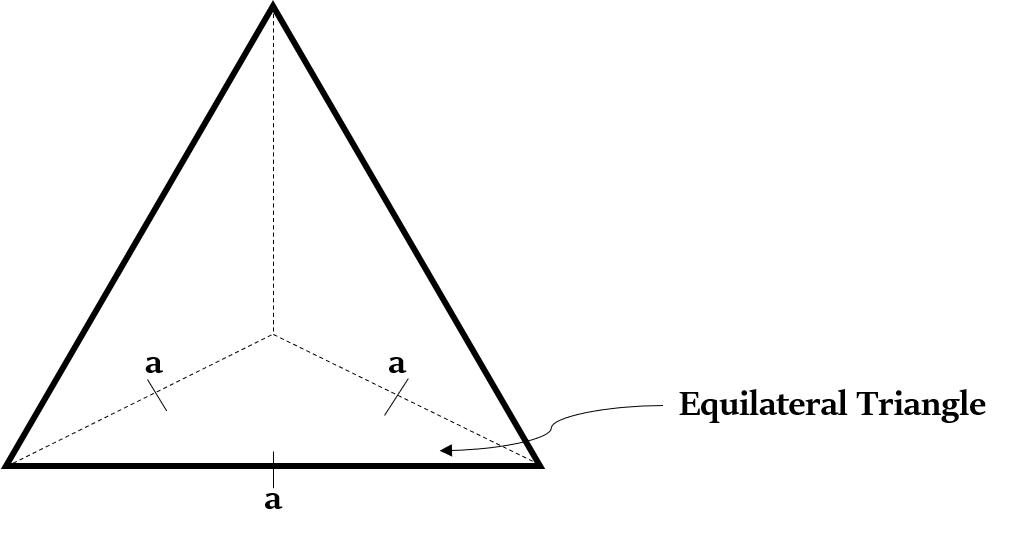

Mensuration

लम्ब सम-त्रिकोणीय चतुष्फलक से संबंधित सूत्र (Formulae related to Right Equi-triangular Tetrahedrons)

सूत्र 1: तिरछी ऊंचाई और तिरछा किनारा (Slant Height and Slant Edge)

यदि h - ऊँचाई, r - समबाहु त्रिभुज (equilateral triangle) आधार की त्रिज्या, R - समबाहु त्रिभुज (equilateral triangle) आधार की परिधि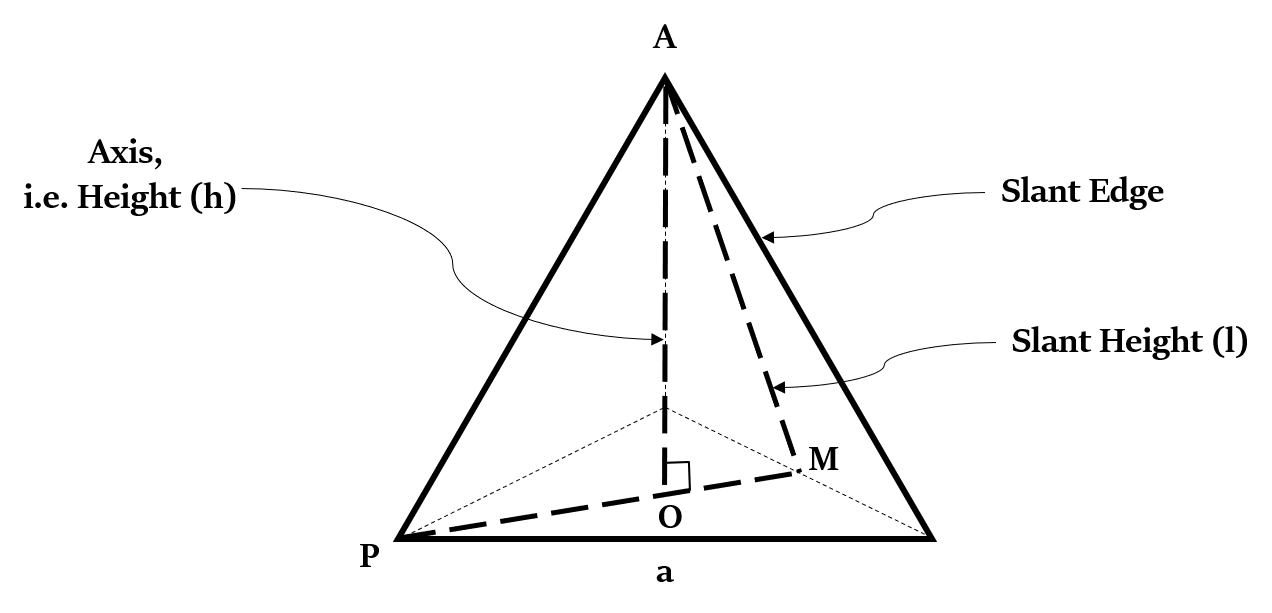

Mensuration

समबाहु त्रिभुज आधार की परिधि (Circumradius), R = $\frac{a}{\sqrt{3}}$
समबाहु त्रिभुज आधार की अंतःत्रिज्या (Inradius), r = $\frac{a}{2 \sqrt{3}}$

पाइथागोरस प्रमेय द्वारा:

तिरछी ऊँचाई (Slant height), l = $\sqrt{h^2 + r^2} = \sqrt{h^2 + (\frac{a}{2 \sqrt{3}})^2}$

तिरछा किनारा (Slant Edge) = $\sqrt{h^2 + R^2} = \sqrt{h^2 + (\frac{a}{\sqrt{3}})^2}$

सूत्र 2: आयतन (Volume)

पिरामिड का आयतन = $\frac{1}{3}$ × आधार क्षेत्र × ऊँचाई

तो, एक लम्ब सम-त्रिकोणीय चतुष्फलक (Right Equi-triangular Tetrahedron) का आयतन = $\frac{1}{3}$ × आधार क्षेत्र × ऊँचाई = $\frac{1}{3} × \frac{\sqrt{3}}{4} a^2$ × h

सूत्र 3: पृष्ठीय क्षेत्रफल (Surface Area)

पार्श्व पृष्ठीय क्षेत्रफल (Lateral surface area) = $\frac{1}{2}$ × आधार की परिधि (Perimeter) × तिरछी ऊंचाई (Slant height) = $\frac{1}{2}$ × 3a × l

कुल पृष्ठीय क्षेत्रफल (Total surface area) = पार्श्व पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल = $\frac{1}{2} × 3a × l + \frac{\sqrt{3}}{4} a^2$

लम्ब वर्गाकार पिरामिड क्या होता है? (What is a Right Square Pyramid?)

लम्ब वर्गाकार पिरामिड का आधार एक वर्ग होता है। इसके शेष फलक सर्वांगसम (बिल्कुल समान) समद्विबाहु/isosceles या समबाहु/equilateral त्रिभुज होते हैं। अतः, इसका शीर्ष अपने आधार के केंद्र के ठीक ऊपर ही होता है।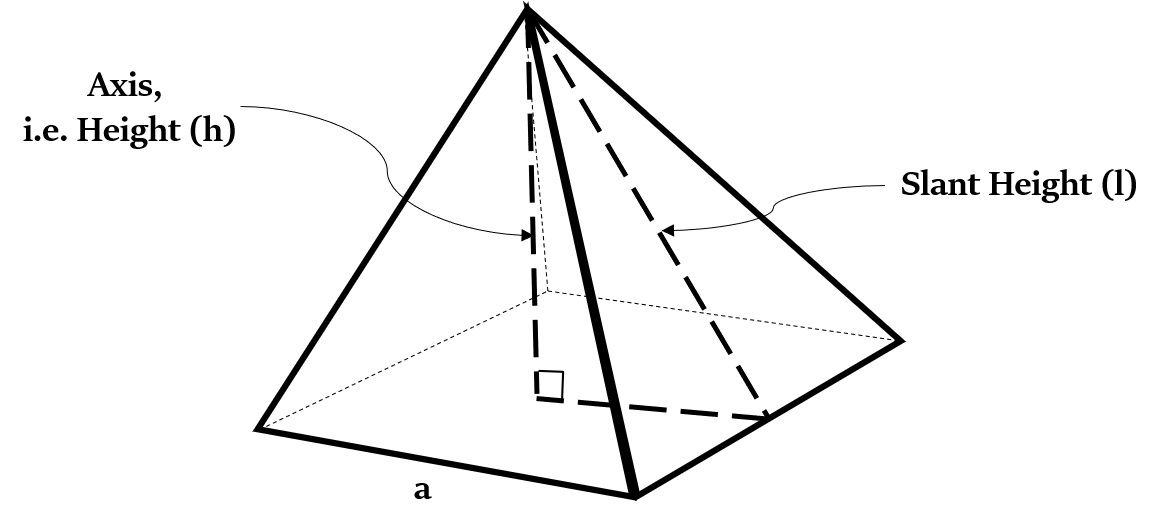

Mensuration

लम्ब वर्गाकार पिरामिड से संबंधित सूत्र (Formulae related to Right Square Pyramid)

सूत्र 1: तिरछी ऊंचाई और तिरछा किनारा (Slant Height and Slant Edge)

यदि h - ऊँचाई, a - आधार वर्ग की भुजा, l - तिरछी ऊँचाई (slant height)

वर्ग आधार की अंत:त्रिज्या (Inradius), r = $\frac{a}{2}$
वर्ग आधार की परिधि (Circumradius), R = $\frac{a}{\sqrt{2}}$

पाइथागोरस प्रमेय द्वारा:

तिरछी ऊँचाई (Slant height), l = $\sqrt{h^2 + r^2} = \sqrt{h^2 + (\frac{a}{2})^2}$

तिरछा किनारा (Slant Edge) = $\sqrt{h^2 + R^2} = \sqrt{h^2 + (\frac{a}{\sqrt{2}})^2}$

सूत्र 2: आयतन (Volume)

पिरामिड का आयतन = $\frac{1}{3}$ × आधार क्षेत्र × ऊँचाई

अतः, एक लम्ब वर्गाकार पिरामिड (Right Square Pyramid) का आयतन = $\frac{1}{3}$ × आधार क्षेत्र × ऊँचाई = $\frac{1}{3} × a^2$ × h

सूत्र 3: पृष्ठीय क्षेत्रफल (Surface Area)

पार्श्व पृष्ठीय क्षेत्र (Lateral surface area) = $\frac{1}{2}$ × आधार की परिधि × तिरछी ऊंचाई = $\frac{1}{2}$ × 4a × l

कुल पृष्ठीय क्षेत्रफल (Total surface area) = पार्श्व पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल = $\frac{1}{2} × 4a × l + a^2$

लम्ब षट्कोणीय पिरामिड क्या होता है? (What is a Right Hexagonal Pyramid?)

लम्ब षट्कोणीय पिरामिड का आधार एक षट्भुज होता है। इसके शेष फलक सर्वांगसम (बिल्कुल समान) समद्विबाहु या समबाहु त्रिभुज होते हैं। अतः, इसका शीर्ष अपने आधार के केंद्र के ठीक ऊपर ही होता है।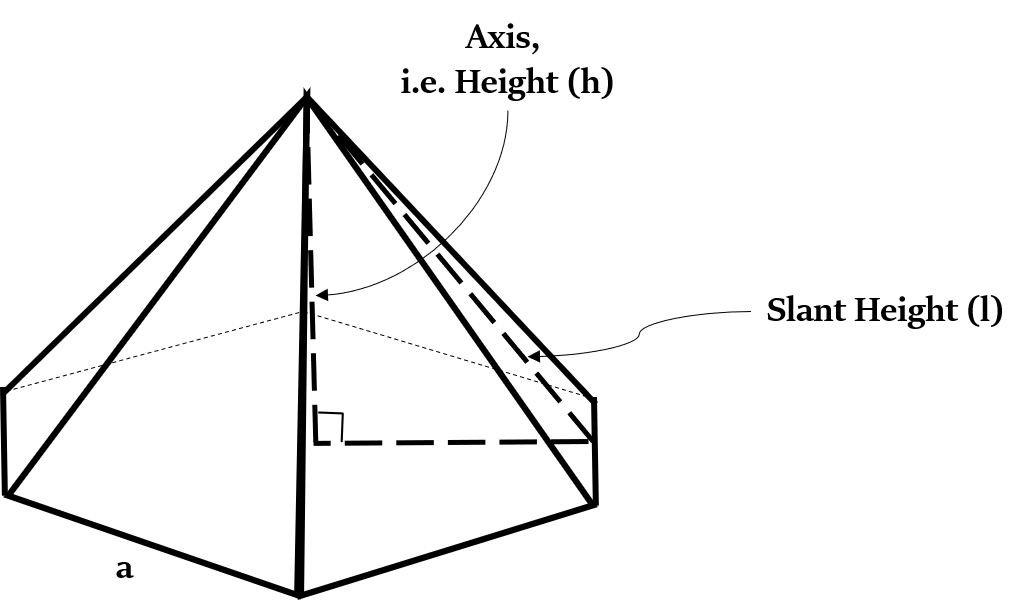

Mensuration

लम्ब षट्कोणीय पिरामिड से संबंधित सूत्र (Formulae related to Right Hexagonal Pyramid)

सूत्र 1: तिरछी ऊंचाई और तिरछा किनारा (Slant Height and Slant Edge)

यदि h - ऊँचाई, a - आधार षट्भुज (hexagon) की भुजा, l - तिरछी ऊँचाई (slant height)

षट्भुज आधार की अंतःत्रिज्या (Inradius), r = $\frac{\sqrt{3}}{2}$ a

पाइथागोरस प्रमेय द्वारा:

तिरछी ऊँचाई (Slant height), l = $\sqrt{h^2 + r^2} = \sqrt{h^2 + (\frac{\sqrt{3}a}{2})^2}$

तिरछा किनारा (Slant Edge) = $\sqrt{h^2 + R^2} = \sqrt{h^2 + a^2}$

सूत्र 2: आयतन (Volume)

पिरामिड का आयतन = $\frac{1}{3}$ × आधार क्षेत्र × ऊँचाई

अतः, लम्ब षट्कोणीय पिरामिड का आयतन = $\frac{1}{3}$ × आधार क्षेत्र × ऊँचाई = $\frac{1}{3} × \frac{6\sqrt{3}}{4}a^2$ × h

सूत्र 3: पृष्ठीय क्षेत्रफल (Surface Area)

पार्श्व पृष्ठीय क्षेत्रफल = $\frac{1}{2}$ × आधार की परिधि × तिरछी ऊंचाई = $\frac{1}{2}$ × 6a × l

कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल = $\frac{1}{2} × 6a × l + \frac{6\sqrt{3}}{4} a^2$