समानुपात की मूल अवधारणाएँ (Basic Concepts of Proportion)

Overview

इस लेख में हम क्वांटिटेटिव एप्टीटुड (गणित) के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Basic Concepts of Proportion, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• Ratio
• Partnership

यदि दो अनुपात बराबर हैं, तो हम कहते हैं कि वे समानुपात में हैं। प्रतीक '::' या '=' का प्रयोग दो समान अनुपातों को निरूपित करने के लिए किया जाता है।

जैसे की, a : b :: b : c या a : b :: c : d

सामान्य समानुपात (Normal Proportion)

आइए, चार मात्राओं के सामान्य समानुपात पर विचार करें।

चार राशियों को सामान्य समानुपात (या सिर्फ समानुपात) में कहा जाता है, यदि पहली और दूसरी मात्रा का अनुपात तीसरी और चौथी मात्रा के अनुपात के बराबर हो।

a : b = c : d या a : b : : c : d (सामान्य समानुपात)

यहाँ पहले और चौथे पद को चरम/बाहरी पदों (a और d) के रूप में जाना जाता है। दूसरे और तीसरे पदों को मध्य पद (b और c) के रूप में जाना जाता है।

तो, a/b = c/d
या, ad = bc
अर्थात्, बाहरी पदों का गुणनफल (ad) = मध्य पदों का गुणनफल (bc)

सामान्य समानुपात के गुण (Properties of Normal Proportion)

यदि चार राशियाँ a, b, c और d सामान्य समानुपात में हैं तो:

Invertendo

यदि a/b = c/d, तो b/a = d/c

Alternando

यदि a/b = c/d , तो a/c = b/d

Componendo

यदि a/b = c/d, तो (a + b)/b = (c + 𝑑)/d

Dividendo

यदि a/b = c/d, तो (a − b)/b = (c − d)/d

Componendo and dividendo

यदि a/b = c/d, तो (a + b)/(a − b) = (c + d)/(c − d)
इसका उल्टा भी सत्य है - यदि (a + b) / (a ​​- b) = (c + d)/(c - d), तो हम यह निष्कर्ष निकाल सकते हैं कि a/b = c/d

एक विशेष गुण

$a/b = c/d = e/f....... = ak_1 + ck_2 + ek_3 +...../bk_1 + dk_2 + fk_3$ +.....

(जहां $k_1, k_2, k_3$… वास्तविक संख्याएं हैं, जोकि सभी एक साथ शून्य नहीं हो सकती हैं)

एक विशेष संबंध:

जब $k_1 = k_2 = k_3$… = 1

निरंतर समानुपात (Continued Proportion)

तीन मात्राओं का निरंतर समानुपात (Continued Proportion of three quantities)

तीन मात्राएँ निरंतर समानुपात में कहलाती हैं, यदि पहली और दूसरी मात्रा का अनुपात दूसरी और तीसरी मात्रा के अनुपात के बराबर हो।

a : b = b : c या a : b : : b : c

यहां पहले और तीसरे पदों को चरम/बाहरी पदों (a और c) के रूप में जाना जाता है। दूसरा पद मध्य पद (b) के रूप में जाना जाता है।

तो, a/b = b/c

या $b^2$ = ac

b को a और c का औसत आनुपातिक (mean proportional) कहा जाता है।

a, b, और c गुणोत्तर श्रेढ़ी (Geometric Progression) में हैं, जैसे की 1, 4, 16 ($4^2$ = 1 × 16)

चार मात्राओं का निरंतर समानुपात (Continued Proportion of four quantities)

चार मात्राओं को निरंतर समानुपात में कहा जाता है, यदि:
a : b = b : c = c : d

तो, a/b = b/c = c/d

या, $b^2$ = ac और $c^2$ = bd

a, b, c, d गुणोत्तर श्रेढ़ी (Geometric Progression) में हैं, जैसे की 1, 4, 16, 64 ($4^2 = 1 × 16; 16^2$ = 4 × 64)

इन तीनों अनुपातों को गुणा करके हम a : d प्राप्त कर सकते हैं।
a/d = a/b × b/c × c/d

चार समानुपात (Four Proportions)

यदि a/b = b/c, तो:

• a = $\frac{b^2}{c}$ पहला समानुपात (first proportional)

• b = √ac - दूसरा समानुपात या गुणोत्तर माध्य (geometric mean)

• c = $\frac{b^2}{a}$ - तीसरा समानुपात (third proportional)

यदि a/b = c/d, तो:

• d = bc/a - चौथा समानुपात (fourth proportional)

नोट

पहला समानुपात × चौथा समानुपात = दूसरा समानुपात × तीसरा समानुपात

समानुपात में वेरिएशन क्या होता है? (What is Variation in Proportions?)

दो मात्राएँ ऐसी हो सकती हैं, कि जैसे ही एक मात्रा में परिवर्तन होता है, दूसरी मात्रा में भी परिवर्तन होता है। ऐसा सम्बन्ध कई प्रकार का हो सकता है:

• सीधा समानुपात (Directly Proportional)
• सीधा सम्बन्ध (Directly Related)
• व्युक्रमानुपाती (Inversely Proportional)
• उल्टा सम्बन्ध (Inversely Related)
• उपरोक्त का मिश्रण (Joint Variation)

Direct Variation

यह दो प्रकार का हो सकता है: सीधा समानुपात (Directly Proportional) and सीधा सम्बन्ध (Directly Related)

सीधा समानुपात (Directly Proportional)

एक राशि B दूसरी राशि A के सीधे समानुपाती होती है, यदि उनका संबंध ऐसा है कि यदि A को एक निश्चित अनुपात में बढ़ाया जाता है, तो B भी उसी अनुपात में बढ़ता है और यदि A को एक निश्चित अनुपात में घटाया जाता है, तो B भी उसी अनुपात में घटता है।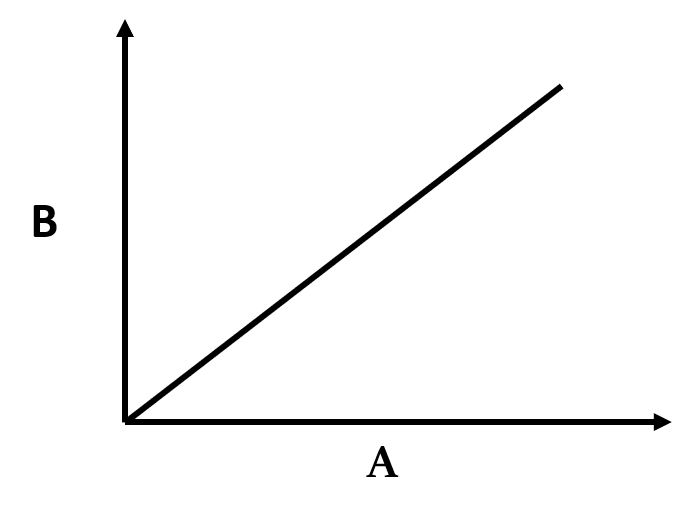

directly proportional

उदाहरण के लिए, अगर A तीन गुना हो जाता है, B भी तीन गुना हो जाता है| और अगर A 2.6 गुना हो जाता है, तो B भी 2.6 गुना हो जाता है|

सीधे अनुपात के संबंध को B α A के रूप में दर्शाया जाता है।

सीधे आनुपातिक का मतलब है की अनुपात स्थिर है (Directly Proportional means Ratio is constant)

यदि B α A, तो B = kA, जहाँ k एक स्थिरांक है। (आनुपातिकता, अर्थार्थ proportionality का स्थिरांक)
तो, B/A = k, यानि दो मात्राओं का अनुपात स्थिर है।
इसके विपरीत, जब दो राशियों का अनुपात स्थिर होता है, तो हम यह निष्कर्ष निकाल सकते हैं कि वे एक दूसरे के साथ सीधे आनुपातिक हैं।

सीधे आनुपातिक चरों के दो जोड़े (Two pairs of directly proportional variables)

यदि B, A के साथ सीधे आनुपातिक है, अर्थार्थ B α A, तो हम लिख सकते हैं:
B1/A1 = B2/A2
या, B1/B2 = A1/A2

सीधे आनुपातिक के वास्तविक जीवंत उदाहरण (Real-life examples of of direct proportion)

सीधे आनुपातिक के कुछ उदाहरण निम्नलिखित हैं:

a. व्यय α मूल्य प्रति इकाई (यदि खरीदी गई इकाइयों की संख्या स्थिर है)

b. किए गए कार्य की मात्रा α काम करने वाले पुरुषों की संख्या (अगर कार्य की दर, और वो समय जिसके लिए किया गया कार्य किया गया हो, स्थिर रहता है)

c. तय की गई दूरी α गति (अगर समय समान हो)

प्र. किसी एडवेंचर पार्क में सवारी का खर्च उस पर सवार लोगों की संख्या के समानुपाती होता है। जब 15 लोग सवारी करते हैं तो खर्चा रु. 300 होता है| अगर 45 लोग सवारी करते हैं, तो खर्च क्या होगा?

व्याख्या:

सीधे आनुपातिक के विशेष मामले (Special Cases of direct proportion)

एक मात्रा B, A की किसी घात के भी सीधे समानुपाती हो सकती है।

अर्थात्, B α $A^n$ या B = k $A^n$

तो, अनुपात $\frac{B}{A^n}$ = k (अर्थात सतत)

प्र. एक लड़के की लंबाई उसकी उम्र के वर्गमूल के सीधे अनुपात में है। यदि 4 वर्ष की आयु में वह 2 फीट लंबा था, तो 12 वर्ष बाद उसकी ऊंचाई क्या होगी?

व्याख्या:

सीधा सम्बन्ध (Directly Related)

यदि B, A से सीधे संबंधित, अर्थार्थ directly related है (सीधे आनुपातिक, अर्थार्थ directly proportional नहीं), तो जैसे-जैसे A बढ़ता है, B भी बढ़ता है, लेकिन आनुपातिक (proportionally) रूप से नहीं।

B = $k_1 A + k_2$
(जहां $k_1$ और $k_2$ स्थिरांक हैं।)

सीधे अनुपात में रेखा मूल निर्देशांक (origin) से गुजरती है (अर्थात जब A का मान शून्य होता है, B भी शून्य होता है)।
लेकिन सीधे संबंध के मामले में, भले ही A = 0 हो, B शून्य नहीं होता है।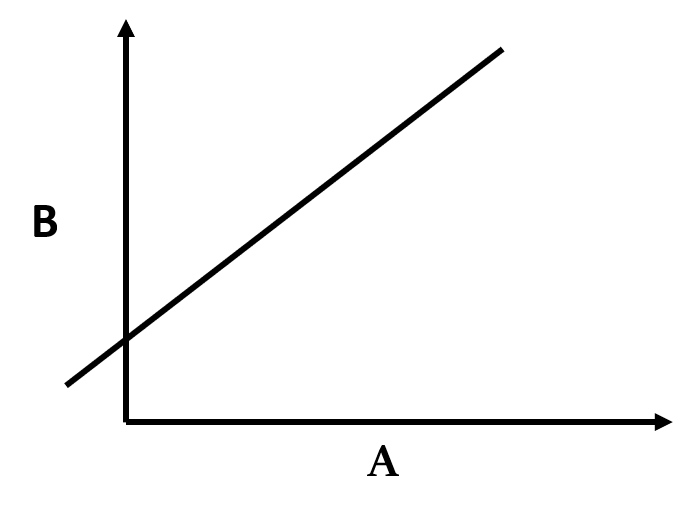

directly related

सीधे आनुपातिक के वास्तविक जीवंत उदाहरण (Real-life examples of of direct relation)

उत्पादन की कुल लागत = निश्चित लागत + परिवर्तनीय लागत = निश्चित लागत + (प्रति इकाई लागत × उत्पादित इकाइयों की संख्या)

कुल कैब किराया = निश्चित लागत + (किराया प्रति किमी × यात्रा किये गए किलोमीटर की संख्या)

परिवर्तनीय लागत - प्रति यूनिट लागत (यह खर्चा तभी होगा जब कोई इकाई उत्पादित होती है) या किराया प्रति किमी (केवल कैब चलने पर ही देना होगा)

निश्चित लागत - यह लागत लगेगी, भले ही कोई इकाई उत्पादित न हो (जैसे जगह का किराया, मशीनरी की लागत, वेतन) या कैब बिलकुल भी न चले, तब भी।

प्र. एडवेंचर पार्क में राइड है। जब 10 लोग सवारी करते हैं तो खर्च रु. 300 आता है, जबकि जब 15 लोग सवारी करते हैं तो खर्च रु. 400 आता है| अगर 25 लोग सवारी करते हैं, तो क्या खर्च होगा?

व्याख्या:

Inverse Variation

यह दो प्रकार का हो सकता है: व्युक्रमानुपाती (Inversely Proportional) और उल्टा सम्बन्ध (Inversely Related)

व्युक्रमानुपाती (Inversely Proportional)

एक मात्रा B दूसरी मात्रा A के व्युत्क्रमानुपाती होती है, यदि उनका संबंध ऐसा है कि यदि A को एक निश्चित अनुपात में बढ़ाया जाता है, तो B उसी अनुपात में कम हो जाता है, और यदि A को एक निश्चित अनुपात में घटा दिया जाता है, तो B भी उसी अनुपात में बढ़ जाता है।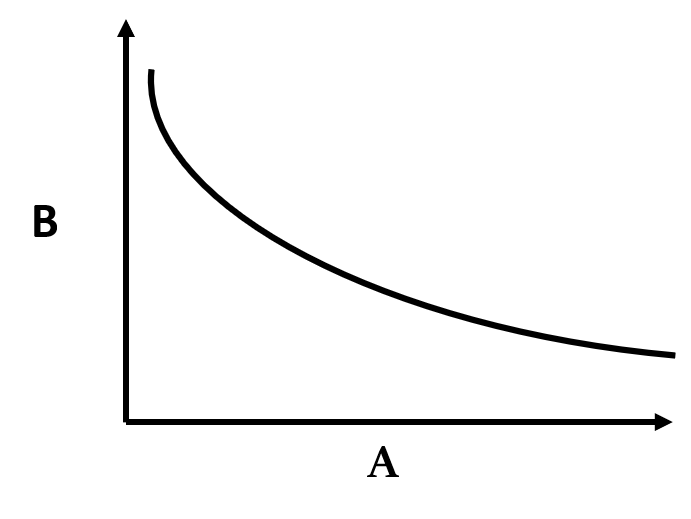

inversely proportional

व्युत्क्रमानुपाती का अर्थ है की गुणनफल अचल है (Inversely Proportional means Product is constant)

B का A के व्युत्क्रमानुपाती होना, यह कहने के समान है कि B 1/A के साथ सीधे अनुपात में बदलता है।
तो, B α 1/A
या B = k/A, जहां k आनुपातिकता का स्थिरांक है।
अत:, AB = k (एक अचर)

इसके विपरीत, यदि दो राशियों का गुणनफल एक स्थिरांक हो, तो हम यह निष्कर्ष निकाल सकते हैं कि वे एक-दूसरे के साथ व्युत्क्रमानुपाती हैं।

व्युत्क्रमानुपाती चरों के दो जोड़े (Two pairs of inversely proportional variables)

यदि B, A के साथ व्युत्क्रमानुपाती रूप से बदलता है, अर्थार्थ B α 1/A, तो:
A1 B1 = A2 B2
या A1/A2 = B2/B1

व्युक्रमानुपात के वास्तविक जीवंत उदाहरण (Real-life examples of of inverse proportion)

व्युत्क्रम अनुपात (Inverse Proportion) के कुछ उदाहरण निम्नलिखित हैं:

a. लोगों की संख्या जितनी अधिक होगी, किसी दिए गए कार्य को पूरा करने में उतना ही कम समय लगेगा।

b. गति बढ़ने पर, दूरी तय करने में लगने वाला समय आनुपातिक रूप से कम हो जाता है (यदि दूरी स्थिर हो)।

प्र. यदि 10 आदमी 20 दिनों में एक दीवार बना सकते हैं, तो 25 आदमी इसे कितने दिनों में बनाएंगे?

व्याख्या:

सीधे अनुपात के विशेष मामले (Special Cases of direct proportion)

एक मात्रा B, A की किसी घात के भी व्युत्क्रमानुपाती हो सकती है।

यानी, B α $\frac{1}{A^n}$
या B $A^n$ = k (अर्थात अचल)

उल्टा सम्बन्ध (Inversely Related)

यदि B उलटे रूप से A के साथ संबंधित है, तो जैसे-जैसे A बढ़ता है (या घटता है), तो वैसे-वैसे B घटता है (या बढ़ता है), लेकिन उसी अनुपात में नहीं।

B = $\frac{k_1}{A} + k_2$
(जहां $k_1$ और $k_2$ स्थिरांक हैं।)

Joint Variation

एक चर एक ही समय में एक से अधिक चरों के समानुपाती (proportional) हो सकता है।

आइए कुछ मामलों को देखें:

केस 1

यदि तीन मात्राएँ A, B और C इस प्रकार हैं कि:
A α B (यदि C अचल हो) और
A α C (यदि B अचल हो)

तो, A α BC (अर्थात A, B और C के साथ संयुक्त रूप से बदलता है)
या A = kBC (जहाँ k आनुपातिकता, अर्थार्थ proportionality का स्थिरांक है)

केस 2

यदि तीन मात्राएँ A, B और C इस प्रकार हैं कि:
A α B और A α 1/C

तो, A α B/C या A = kB/C या AC/B = k (जहाँ k आनुपातिकता, अर्थार्थ proportionality का स्थिरांक है)