क्षेत्रमिति - शंकु (Mensuration - Cone)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Cone, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• क्षेत्रमिति क्या होती है?
• क्षेत्रमिति - घन और घनाभ
• क्षेत्रमिति - गोला
• क्षेत्रमिति - बेलन
• क्षेत्रमिति - शंकु
• क्षेत्रमिति - प्रिज्म
• क्षेत्रमिति - पिरामिड

इस लेख में, हम क्षेत्रमिति के एक महत्वपूर्ण विषय, शंकु से संबंधित अवधारणाओं और सूत्रों के बारे में जानने जा रहे हैं।

शंकु क्या होता है? (What is a Cone?)

शंकु एक त्रिविमीय ठोस संरचना है, जिसका आधार एक वृत्त है और इसका एक शीर्ष (vertex) है।

सबसे प्रसिद्ध प्रकार का शंकु है लंब वृत्तीय शंकु (Right Circular Cone)। यह एक ऐसा शंकु है जिसका शीर्ष सीधे इसके आधार वृत्त के केंद्र के ऊपर होता है।

Mensuration

नोट

जब आप किसी वृत्त के समकोण त्रिज्यखंड (right-angled sector) या वृत्त के अर्धवृत्ताकार त्रिज्यखंड (semicircular sector) को घुमाते हैं, तो आपको आधार के बिना एक शंकु प्राप्त होता है।

शंकु से जुड़े सूत्र (Formulae related to Cone)

यदि 'r' इसके आधार की त्रिज्या (radius) है, 'h' इसकी ऊँचाई है, और 'l' इसकी तीयर्क ऊँचाई (slant height) है, तो: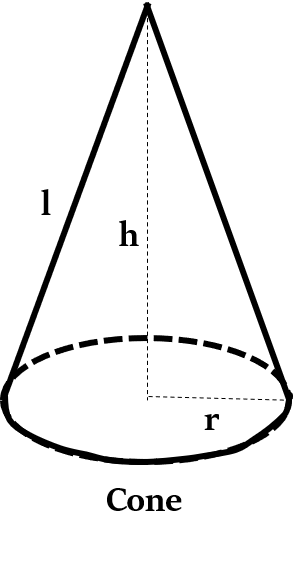

Mensuration

सूत्र 1: आयतन (Volume)

शंकु का आयतन = $\frac{1}{3}$ x आधार का क्षेत्रफल x ऊँचाई = $\frac{1}{3} πr^2 h$

सूत्र 2: पृष्ठीय क्षेत्रफल (Surface Area)

शंकु का पार्श्व पृष्ठीय क्षेत्रफल (Lateral/Curved Surface area) = $\frac{1}{2}$ x आधार का परिमाप/Perimeter x तीयर्क ऊँचाई = rl

नोट

शंक्वाकार तम्बू के निर्माण के लिए आवश्यक कैनवास = शंकु का वक्र/पार्श्व पृष्ठीय क्षेत्रफल (Curved surface area)

शंकु का कुल पृष्ठीय क्षेत्रफल (Total Surface area) = पार्श्व पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल = π rl + π $r^2$ = π r(l + r)

नोट

तीयर्क ऊँचाई (Slant height), l = $\sqrt{r^2 + h^2}$

सूत्र 3: शंकु का छिन्नक (Frustum of a Cone)

छिन्नक एक 3-D ठोस आकृति का वह भाग है जो इसे काटने वाले एक या दो समानांतर तलों के बीच स्थित होता है।

उदाहरण के लिए, शंकु का छिन्नक, पिरामिड का छिन्नक आदि।

एक शंकु का छिन्नक प्राप्त करने के लिए, हम इसे इसके आधार के समानांतर एक समतल द्वारा काटते हैं। इस तल और मूल शंकु के आधार के बीच ठोस का भाग शंकु के छिन्नक के रूप में जाना जाता है।

Mensuration

शंकु के छिन्नक का आयतन (Volume of the frustum of the cone) = $\frac{1}{3} πh (r_1^2 + r_2^2 + r_1r_2)$

शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल (Curved surface area of frustum of cone) = $π(r_1 + r_2)s$, जहाँ s = $\sqrt{h^2 + (r_1 - r_2)^2}$

शंकु के छिन्नक का कुल पृष्ठीय क्षेत्रफल (Total surface area of frustum of cone) = $πs (r_1 + r_2)+ πr_1^2 + πr_2^2$, जहाँ s = $\sqrt{h^2 + (r_1 - r_2)^2}$