करणी क्या होते हैं? (What are Surds?)

Jan 3, 2022 simplification
Share on:
करणी क्या होते हैं? (What are Surds?)

Overview

इस लेख में हम क्वांटिटेटिव एप्टीटुड (गणित) के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - What are Surds?, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

करणी (Surds) एक प्रकार की अपरिमेय संख्याएँ (irrational numbers) हैं।

सभी करणी (Surds) अपरिमेय संख्याएँ होते हैं, लेकिन इसका विपरीत सत्य नहीं है। अर्थात्, सभी अपरिमेय संख्याएँ करणी (Surds) नहीं होती हैं। उदाहरण के लिए, π, e आदि अपरिमेय संख्याएँ हैं, लेकिन करणी (Surds) नहीं हैं।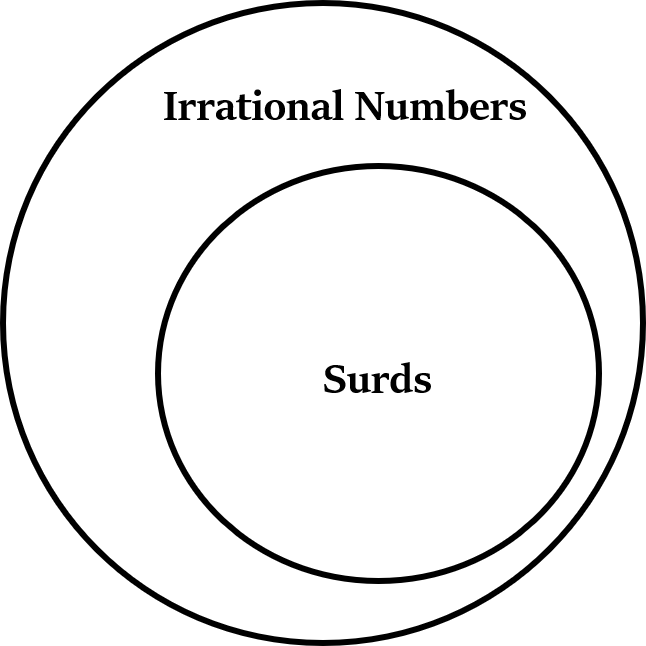
Simplification

Simplification

अतः, हम कह सकते हैं कि करणी (Surds) अपरिमेय संख्याओं का एक उपसमुच्चय है।

नोट

परिमेय संख्याएँ (Rational numbers) - वे संख्याएँ जिन्हें p/q के रूप में लिखा जा सकता है, जहाँ p और q पूर्णांक (integers) हैं और q ≠ 0
अन्य सभी संख्याएँ अपरिमेय संख्याएँ हैं।

an\sqrt[n]{a} कोटि n का करणी (surd of order n) है, यह देखते हुए कि यह एक अपरिमेय संख्या है (a एक परिमेय संख्या है, और n एक धनात्मक पूर्णांक है)

आइए कुछ उदाहरण देखें।

  • कोटि 2 का करणी, यानी जब n = 2 (जिसे द्विघात करणी, Quadratic Surds भी कहा जाता है)। उदाहरण के लिए, 5\sqrt{5}, 63\sqrt{3}, आदि।

  • कोटि 3 का करणी, यानी जब n = 3. उदाहरण के लिए, 53\sqrt[3]{5}, 573\sqrt[3]{7} आदि।

  • और इसी तरह आगे भी ....
नोट

4\sqrt{4} (= 2), 273\sqrt[3]{27} (= 3) जैसे व्यंजक करणी नहीं हैं, क्योंकि वे परिमेय संख्याएं हैं।

हम ज्यादातर द्विघात करणी के साथ ही काम करेंगे, यानी वर्गमूल टर्म वाले करणी (कोई उच्च मूल नहीं), यानी a\sqrt{a}, जहां a एक परिमेय संख्या (rational number) है, लेकिन पूर्ण वर्ग (perfect square) नहीं है।

हम उन व्यंजकों पर भी विचार करेंगे जिनमें परिमेय संख्याओं और करणी का मिश्रण होता है। उदाहरण के लिए, a + b\sqrt{b}, a + b\sqrt{b} + c\sqrt{c} आदि।

यदि कोई करणी व्यंजक a + b\sqrt{b} के रूप का है, तो इसका संयुग्म ± (a - b\sqrt{b}) होगा।

एक विषम व्यंजक और उसके संयुग्म का गुणनफल हमेशा एक परिमेय संख्या होती है।

आइए, अब हम करणी (surds) के नियमों पर एक नज़र डालें, जो हमें करणी से जुड़े व्यंजकों को सरल और हल करने में मदद करेंगे।

an=a1n\sqrt[n]{a} = a^\frac{1}{n}

anm=anm=a1nm\sqrt[m]{\sqrt[n]{a}} = \sqrt[nm]{a} = \sqrt{a^\frac{1}{nm}}

(an)m=amn(\sqrt[n]{a})^m = \sqrt[n]{a^m}

नोट

(an)n=ann(\sqrt[n]{a})^n = \sqrt[n]{a^n} = a

a×b=ab\sqrt{a} × \sqrt{b} = \sqrt{ab}

ab=ab\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}

an×bn=abn\sqrt[n]{a} × \sqrt[n]{b} = \sqrt[n]{ab}

anbn=abn\frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}}

अगर a + b\sqrt{b} = c + d\sqrt{d}, तो:

a = c (अर्थात द्विघात करणी व्यंजकों के परिमेय भाग बराबर होंगे)
b = d (अर्थात द्विघात करणी व्यंजकों के अपरिमेय भाग बराबर होंगे)
नोट

यदि a + b=d\sqrt{b} = \sqrt{d}, तो a = 0 और b = d
यदि a + b\sqrt{b} = c, तो a = c और b = 0

a.a.a...nबार=a(1−12n)\sqrt{a . \sqrt{a . \sqrt{a \hspace{1ex}...n \hspace{1ex} बार}}} = a^{(1 - \frac{1}{2^n})}

नोट

तो, जब n = ∞,

a.a.a...∞\sqrt{a . \sqrt{a . \sqrt{a \hspace{1ex}...∞}}} = a

यदि, a+a+a...∞\sqrt{a + \sqrt{a + \sqrt{a \hspace{1ex}...∞}}} = p, तो p(p - 1) = a

कभी-कभी हमें भिन्नों के हर (denominator) में करणी मिलते हैं। उदाहरण के लिए, 1a+b\frac{1}{a + \sqrt{b}}

इस पर काम करना मुश्किल है। इसलिए, हम करणी को rationalize करते हैं, जो भिन्न के मान को बदले बिना, हर में करणी को परिमेय संख्या में बदलने की प्रक्रिया है।

ऐसा करने के लिए, हम भाजक और हर दोनों को, हर में उपस्थित करणी के संयुग्म से गुणा करते हैं। इसलिए, हम 1a+b\frac{1}{a + \sqrt{b}} के अंश और हर को ± (a - b\sqrt{b}) से गुणा करेंगे, अर्थात या तो (a - b)\sqrt{b)}) से या (- a + b\sqrt{b}) से

नोट

यदि करणी 1a+b+c\frac{1}{a + \sqrt{b} + \sqrt{c}} प्रकार का है, तो हमें इस प्रक्रिया को दो बार दोहराना होगा।

एक उदाहरण से यह बात और स्पष्ट हो जाएगी।

13−11\frac{1}{3 - \sqrt{11}}

Explanation:

दिए गए भिन्न व्यंजक का हर 3−113 - \sqrt{11} है। इसके संयुग्म 3+113 + \sqrt{11} और −3−11- 3 - \sqrt{11} हैं।

आइए 3+113 + \sqrt{11} लेते हैं, और दिए गए भिन्न व्यंजक के अंश और हर दोनों को इससे गुणा करते हैं।

13−11×3+113+11=3+1132−11\frac{1}{3 - \sqrt{11}} × \frac{3 + \sqrt{11}}{3 + \sqrt{11}} = \frac{3 + \sqrt{11}}{3^2 - 11} = 3+119−11=3+11(−2)\frac{3 + \sqrt{11}}{9 - 11} = \frac{3 + \sqrt{11}}{(-2)}


a + b\sqrt{b} प्रकार के करणी का वर्गमूल x+y\sqrt{x} + \sqrt{y} के रूप में होगा।

आइए कुछ तरीकों को देखें जिनका उपयोग हम a + b\sqrt{b} प्रकार के करणी का वर्गमूल निकालने के लिए कर सकते हैं।

हम निम्नलिखित की बराबर रख सकते हैं:

a + b=(x+y)2\sqrt{b} = (\sqrt{x} + \sqrt{y})^2

x और y के लिए हल करें।

ध्यान दें कि परिमेय और अपरिमेय दोनों तरह के पदों वाले किसी भी समीकरण में, दोनों पक्षों के परिमेय भाग समान होते हैं, और दोनों पक्षों के अपरिमेय भाग भी समान होते हैं।

दिए गए करणी को (x+y)2(\sqrt{x} + \sqrt{y})^2 या (x−y)2(\sqrt{x} - \sqrt{y})^2 के रूप में लिखें।

यदि हम ऐसा कर सकते हैं, तो यह स्पष्ट है कि दिए गए करणी का वर्गमूल क्रमशः (x+y\sqrt{x} + \sqrt{y}) या (x−y\sqrt{x} - \sqrt{y}) होगा|

नोट

हम a + b\sqrt{b} प्रकार के करणी को, अर्थात जिसका अपरिमेय भाग धनात्मक है, इस प्रकार लिखेंगे (x+y)2(\sqrt{x} + \sqrt{y})^2
हम a - b\sqrt{b} प्रकार के करणी को, अर्थात जिसका अपरिमेय भाग ऋणात्मक है, इस प्रकार लिखेंगे (x−y)2(\sqrt{x} - \sqrt{y})^2

एक उदाहरण से यह बात और स्पष्ट हो जाएगी।

24 + 411\sqrt{11}

व्याख्या:

चूँकि दिए गए करणी का अपरिमेय भाग धनात्मक है, हम (x+y)2(\sqrt{x} + \sqrt{y})^2 के रूप में लिखने का प्रयास करेंगे।

अब, (x+y)2=x2+y+2xy(\sqrt{x} + \sqrt{y})^2 = x^2 + y + 2x\sqrt{y}

हम देख सकते हैं कि अपरिमेय पद का गुणांक (coefficient) 2 है। अतः, इस करणी में भी हम अपरिमेय पद का गुणांक 2 रखेंगे।

तो, 24 + 411\sqrt{11} = 24 + 24×11\sqrt{4 × 11} = 24 + 244\sqrt{44}

अब, हमें ऐसी दो संख्याएँ m और n ज्ञात करने की आवश्यकता है, कि:

  • उनका गुणनफल वर्गमूल के अंदर की संख्या हो, अर्थात 44।
  • उनका योग दिए गए व्यंजक का परिमेय भाग हो, अर्थात 24

हमारे मामले में उपरोक्त दो शर्तों को पूरा करने वाली दो संख्याएं हैं: 2 और 22

तो, 24 + 244\sqrt{44} = 22 + 2 + 222×2\sqrt{22 × 2} = (22+2)2(\sqrt{22} + \sqrt{2})^2

इसलिए, 24 + 411\sqrt{11} का धनात्मक वर्गमूल है:
22+2=2(11+1)\sqrt{22} + \sqrt{2} = \sqrt{2} (\sqrt{11} + 1)


कभी-कभी हमें कुछ करणी की तुलना करने की आवश्यकता हो सकती है।

  • सबसे बड़ा/निम्नतम मान वाला करणी ज्ञात करने के लिए।
  • उन्हें आरोही या अवरोही क्रम में व्यवस्थित करने के लिए।

ऐसा करने के लिए, हम निम्नलिखित चरणों का पालन करते हैं:

चरण 1: हम परिमेय भागों को घटाते हैं। फिर बाकी की तुलना करें।

चरण 2: यदि चीजें अभी भी स्पष्ट नहीं हैं, तो हम नए करणी का वर्ग करते हैं और परिमेय भागों को फिर से घटाते हैं। ज्यादातर मामलों में, हम अब आसानी से करणी की तुलना कर सकते हैं।

हालाँकि, यदि हम ऐसा नहीं कर सकते हैं, तो हम उनका वर्ग करेंगे, और परिमेय भागों को फिर से घटा देंगे। हम इस प्रक्रिया को दोहराएंगे जब तक हम निश्चितता के साथ उनके मूल्यों की तुलना नहीं कर सकते।

आइए, एक उदाहरण देखें।

3 + 22\sqrt{22} और 4 + 14\sqrt{14}

व्याख्या:

यदि हम दो करणी के सन्निकट (approximate) मान ज्ञात करने का प्रयास करें, तो:

  • 3 + 22\sqrt{22} = 3 + 4.कुछ = 7.कुछ

  • 4 + 14\sqrt{14} = 4 + 3.कुछ = 7.कुछ

तो, उनके मूल्य बहुत करीब हैं।

आइए हम समान परिमेय भाग को हटा दें। यदि हम दोनों करणी में से 3 घटाते हैं, तो हमें केवल तुलना करने की आवश्यकता है: 22\sqrt{22} और 1 + 14\sqrt{14} की|

चूंकि चीजें अभी भी बहुत स्पष्ट नहीं हैं, हम दोनों का वर्ग कर सकते हैं। हमें मिल जाएगा:

  • (22)2(\sqrt{22})^2 = 22

  • (1+14)2(1 + \sqrt{14})^2 = 1 + 14 + 214\sqrt{14} = 15 + 214\sqrt{14}

आइए हम समान परिमेय भाग को फिर से हटा दें। यदि हम दोनों करणी में से 15 घटाते हैं, तो हमें केवल तुलना करने की आवश्यकता है: 7 और 214\sqrt{14} की|

चूंकि चीजें अभी भी बहुत स्पष्ट नहीं हैं, हम दोनों को फिर से वर्ग कर सकते हैं। हमें मिल जाएगा:

  • 727^2 = 49

  • (214)2(2\sqrt{14})^2 = 4 × 14 = 56

तो, 4 + 14\sqrt{14} दोनों करणी में से बड़ा है।