सांख्यिकी में केन्द्रीय प्रवृत्ति के माप क्या हैं? (What are Measures of Central tendency in Statistics?)

Jan 8, 2022 statistics

Share on:

सांख्यिकी में केन्द्रीय प्रवृत्ति के माप क्या हैं? (What are Measures of Central tendency in Statistics?)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - What are Measures of Central tendency, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

केंद्रीय प्रवृत्ति के माप (Measures of Central tendency) दिए गए डेटा में एक ऐसे मान को संदर्भित करते हैं, जो कि किसी तरह उस डेटा सेट का केंद्र बिंदु होता है।

डेटा सेट में केंद्रीय बिंदु का पता लगाने के लिए हम विभिन्न तरीकों का उपयोग कर सकते हैं:

माध्य (Mean) - अंकगणित माध्य (Arithmetic mean), ज्यामितीय माध्य (या गुणोत्तर माध्य, Geometric mean), हरात्मक माध्य (Harmonic mean)
माध्यिका (Median)
बहुलक (Mode)

नोट

यदि केवल 'माध्य' लिखा है, तो इसका अर्थ है 'अंकगणित माध्य'।

आइए, अब इन तरीकों का अधिक विस्तार से अध्ययन करें।

अंकगणित माध्य (Arithmetic mean) क्या होता है?

अंकगणित माध्य को माध्य (Mean) या औसत (Average) के रूप में भी जाना जाता है।

यह प्रेक्षणों (observations) के योग को प्रेक्षणों की संख्या से भाग देकर प्राप्त किया जाता है।

अंकगणित माध्य = $\frac{प्रेक्षणों \hspace{1ex} का \hspace{1ex} योग}{प्रेक्षणों \hspace{1ex} की \hspace{1ex} संख्या}$

नोट

अंकगणित माध्य के बारे में अधिक जानने के लिए, आप औसत पर हमारा लेख पढ़ सकते हैं।

माध्य / औसत की गणना के लिए सूत्र (Formulae for calculating the Mean / Average)

अवर्गीकृत डेटा के मामले में (In case of Ungrouped data)

n संख्याओं, $x_1, x_2, x_3, ..... , x_n$ , का माध्य ज्ञात करने के लिए, हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

अंकगणित माध्य = $\frac{x_1 + x_2 + x_3 + ..... + x_n}{n}$

प्र. 3, 4, 5, 6, 7, और 8 का अंकगणितीय माध्य क्या है?

व्याख्या:

अंकगणित माध्य = $\frac{3 + 4 + 5 + 6 + 7 + 8}{6} = \frac{33}{6}$ = 5.5

समूहीकृत डेटा के मामले में (In case of Grouped data)

यदि $x_1, x_2, x_3, ...., x_n$ , $f_1, f_2, f_3, ...., f_n$ की संबंधित आवृत्तियों वाली संख्याएं हैं, तो इसका अर्थ है कि संख्या $x_1$ $f_1$ बार आती है , $x_2$ $f_2$ बार आता है, इत्यादि।

तो, सभी संख्याओं/अवलोकनों के मानों का योग = $f_1 x_1 + f_2 x_2 + ..... + f_n x_n$

प्रेक्षणों की संख्या (अर्थात सभी आवृत्तियों का योग) = $f_1 + f_2 + ..... + f_n$

अंकगणित माध्य = $\frac{f_1 x_1 + f_2 x_2 + ..... + f_n x_n}{f_1 + f_2 + ..... + f_n}$

ज्यामितीय माध्य (Geometric Mean) क्या होता है?

ज्यामितीय माध्य एक ऐसा तरीका है, जो केंद्रीय प्रवृत्ति को प्रदर्शित करने के लिए डेटा मानों के गुणनफल का उपयोग करता है। ज्यामितीय माध्य उनके गुणनफल का $n^{th}$ मूल होता है।

n संख्याओं का ज्यामितीय माध्य ज्ञात करने के लिए, $x_1, x_2, x_3, ...., x_n$ , हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

ज्यामितीय माध्य = $\sqrt[n]{x_1 × x_2 × x_3 × ..... × x_n}$

प्र. 3, 4 और 18 का ज्यामितीय माध्य क्या है?

व्याख्या:

ज्यामितीय माध्य = $\sqrt[3]{3 × 4 × 18} = \sqrt[3]{3^3 × 2^3}$ = 3 × 2 = 6

हरात्मक माध्य (Harmonic Mean) क्या होता है?

हरात्मक माध्य दी गई संख्याओं के व्युत्क्रमों (reciprocal) के अंकगणितीय माध्य का व्युत्क्रम है।

n संख्याओं, $x_1, x_2, x_3, ...., x_n$ , का हरात्मक माध्य ज्ञात करने के लिए हम निम्नलिखित सूत्र का उपयोग कर सकते हैं:

हरात्मक माध्य = $\frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \frac{1}{x_3} + ... + \frac{1}{x_n}}$

प्र. 1, 1/2, और 1/3 का हरात्मक माध्य क्या है?

व्याख्या:

हरात्मक माध्य = $\frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \frac{1}{x_3} + ... + \frac{1}{x_n}} = \frac{3}{1 + 2 + 3} = \frac{3}{6} = \frac{1}{2}$

अंकगणित, ज्यामितीय और हरात्मक माध्यों के बीच संबंध (Relation between Arithmetic, Geometric and Harmonic means)

यदि किन्हीं दो संख्याओं के अंकगणितीय, ज्यामितीय और हरात्मक माध्य क्रमशः A, G और H हैं, तो:

A ≥ G ≥ H
A, G, H, GP में होते हैं, अर्थात $A.H = G^2$

माध्यिका (Median) क्या होता है?

माध्यिका डेटा सेट का मध्य मान है, जब संख्याओं/अवलोकनों को आरोही या अवरोही क्रम में व्यवस्थित किया जाता है।

नोट

माध्यिका ज्ञात करने के लिए, हमें दिए गए आँकड़ों को आरोही या अवरोही क्रम में व्यवस्थित करना चाहिए।

माध्यिका की गणना के लिए सूत्र (Formulae for calculating Median)

अवर्गीकृत डेटा के मामले में (In case of Ungrouped data)

डेटा की संख्या विषम है (Number of data is odd)

यदि हमें n संख्याएँ दी जाती हैं, जहाँ n विषम है, तो बीच की संख्या माध्यिका होगी।

अर्थात्, माध्यिका $\frac{n + 1}{2}^{th}$ संख्या होगी

प्रश्न. {2, 7, 1, 0, और 9} की माध्यिका ज्ञात कीजिए।

व्याख्या:

दिए गए समुच्चय के तत्वों को आरोही क्रम में व्यवस्थित करने पर हमें प्राप्त होता है {0, 1, 2, 7, 9}

माध्यिका $\frac{n + 1}{2}^{th}$ संख्या होगी, अर्थात $\frac{5 + 1}{2}^{th} = 3^{rd}$ संख्या (अर्थात मध्यावधि)

अत: 2 दिए गए समुच्चय की माध्यिका है।

डेटा की संख्या सम है (Number of data is even)

यदि हमें n संख्याएँ दी जाती हैं, जहाँ n सम है, तो बीच में दो संख्याएँ होंगी।

तब माध्यिका $\frac{n}{2}^{th}$ और $(\frac{n}{2} + 1)^{th}$ संख्याओं का माध्य होगी|

प्रश्न. {2, 7, 1, 0, 6, और 9} की माध्यिका ज्ञात कीजिए।

व्याख्या:

दिए गए समुच्चय के तत्वों को आरोही क्रम में व्यवस्थित करने पर हमें प्राप्त होता है {0, 1, 2, 6, 7, 9}

माध्यिका $\frac{n}{2}^{th}$ और $(\frac{n}{2} + 1)^{th}$ संख्याओं का माध्य होगी, यानी $\frac{6}{2 }^{th}$ और $(\frac{6}{2} + 1)^{th}$ संख्याओं, यानी $3^{rd}$ और $4^{th}$ संख्याओं की (अर्थात दो मध्य संख्याओं का माध्य)

अत: दिए गए समुच्चय की माध्यिका = $\frac{2 + 6}{2}$ = 4.

समूहीकृत डेटा के मामले में (In case of Grouped data)

यदि डेटा वर्गों (classes) के रूप में दिया जाता है, तो:

माध्यिका = L + $(\frac{\frac{n}{2} - C.F.}{f})$ × h

L - माध्यिका वर्ग की निचली सीमा (lower limit of the median class)
h - माध्यिका वर्ग का आकार (अर्थात ऊपरी सीमा - निचली सीमा)
f - माध्यिका वर्ग की बारंबारता (frequency of the median class)
C.F. - माध्यिका वर्ग से पहले के वर्ग की संचयी आवृत्ति (Cumulative Frequency of class preceding the median class)
n - कुल आवृत्ति (total frequency)

बहुलक (Mode) क्या होता है?

अवर्गीकृत आँकड़ों (ungrouped data) के मामले में, इसका बहुलक वह संख्या/अवलोकन है जो अधिकतम बार आता है।

समूहीकृत आँकड़ों (grouped data) के मामले में, इसका बहुलक वह संख्या/अवलोकन है जिसकी आवृत्ति सबसे अधिक होती है।

बहुलक की गणना के लिए सूत्र (Formulae for calculating Mode)

अवर्गीकृत डेटा के मामले में (In case of Ungrouped data)

अवर्गीकृत डेटा के मामले में बहुलक/मोड खोजना बहुत आसान है। बस उस संख्या को देखें जो अधिकतम बार आती है।

उदाहरण के लिए, डेटा सेट {1, 4, 3, 6, 7, 3, 4, 6, 3, 5, 8, 3} का बहुलक 3 होगा, क्योंकि यह चार बार आई है, किसी भी अन्य संख्या से अधिक बार।

समूहीकृत डेटा के मामले में (In case of Grouped data)

बहुलक = L + $(\frac{f - f_p}{2f - f_p - f_s})$ × h

L = बहुलक वर्ग की निचली सीमा (lower limit of modal class)
h = वर्ग अंतराल का आकार (सभी वर्ग आकारों को समान मानकर)
f = बहुलक वर्ग की बारंबारता (frequency of the modal class)
$f_p$ = बहुलक वर्ग से पहले के वर्ग की बारंबारता (frequency of the class preceding the modal class)
$f_s$ = बहुलक वर्ग के बाद आने वाले वर्ग की बारंबारता (frequency of the class succeeding the modal class)

नोट

किसी डेटा के सेट में :

एक बहुलक हो सकता है - जैसे की, 1, 3, 5, 6, 4, 6. इसका एक बहुलक है, अर्थात् 6
एक से अधिक बहुलक हो सकते हैं - जैसे की, 1, 3, 5, 6, 4, 6, 1. इसके दो बहुलक हैं, अर्थात् 1 और 6
कोई भी बहुलक बिल्कुल नहीं हो सकता है - जैसे की, 2, 2, 2, 2, 2, 2. इसका कोई बहुलक नहीं है

माध्य, माध्यिका और बहुलक के बीच संबंध (Relation between Mean, Median and Mode)

अंकगणित माध्य (Arithmetic mean) एक डेटा सेट में संख्याओं का औसत (average) है।
बहुलक (Mode) किसी डेटा सेट में सबसे सामान्य संख्या होती है।
माध्यिका (Median) किसी डेटा सेट में, उन संख्याओं के सेट का मध्य होती है (जब उन्हें आरोही या अवरोही क्रम में व्यवस्थित किया जाता है)

अनुभवजन्य संबंध (Empirical relationship)

बहुलक (Mode) = 3 माध्यिका (Median) – 2 माध्य (Mean)

अंकगणित माध्य और माध्यिका के बीच संबंध (Relation between Arithmetic Mean and Median)

जब एक सेट में डेटा समान रूप से वितरित होता है, यानी सेट के किन्हीं दो लगातार तत्वों के बीच का अंतर बराबर होता है (उदाहरण के लिए समान्तर श्रेढ़ी / Arithmetic Progressions के मामले में), तो माध्यिका = अंकगणितीय माध्य

उदाहरण के लिए, संख्याओं 3, 5, 7, 9, 11 पर विचार करें
उपरोक्त समुच्चय में किन्हीं दो तत्वों के बीच का अंतर 2 है। अतः, उनकी माध्यिका और माध्य बराबर होना चाहिए। आइए देखें।
माध्य = (3 + 5 + 7 + 9 + 11)/5 = 35/7 = 7
माध्यिका = मध्य मान, जो कि 7 है।

विषमता (Skewness)

इससे पहले कि हम डेटा वितरण में विषमता को समझें, हमें सामान्य या गैर-विषम डेटा वितरण को समझने की आवश्यकता है।

सममित वितरण क्या होता है? (What is a Symmetric distribution?)

सममित वितरण (Symmetric distribution) को सामान्य वितरण (Normal distribution या Zero-skewed distribution) भी कहा जाता है।

एक सममित वितरण में, वितरण का बायाँ ओर दायाँ हिस्सा एक जैसा होता है, यानी डेटा का वितरण शून्य विषमता दिखाता है। नीचे दिए गए चित्र पर एक नजर डालें: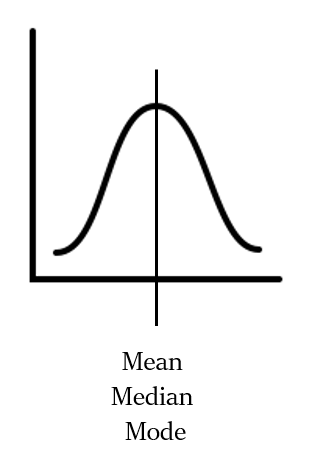
Statistics

Statistics

जैसा कि आप देख सकते हैं, एक सममित वितरण में, माध्य, माध्यिका और बहुलक एक दूसरे के साथ मेल खाते हैं। अर्थात् माध्य = माध्यिका = बहुलक

असममित वितरण क्या होता है? (What is an Asymmetric distribution?)

विषमता किसी सांख्यिकीय वितरण में एक तिरछापन होता है, जिसमें वक्र विकृत या तिरछा दिखाई देता है:

बाईं ओर, या
दांई ओर

तो, दो प्रकार के असममित वितरण होते हैं:

बायाँ विषम वितरण (Left skewed distribution) या ऋणात्मक विषम वितरण (Negative skewed distribution)
दायाँ विषम वितरण (Right skewed distribution) या सकारात्मक विषम वितरण (Positive skewed distribution)

बायाँ विषम वितरण (Left skewed distribution)

वाम/बायाँ विषम वितरण को ऋणात्मक विषम वितरण के रूप में भी जाना जाता है।

बाएं-तिरछे विषम में एक लंबी बाईं पूंछ होती है, यानी संख्या रेखा पर नकारात्मक दिशा में एक लंबी पूंछ होती है। दाहिनी पूंछ छोटी होती है।

यह विषम वितरण इसलिए होता है क्योंकि अधिकांश डेटा मान ऋणात्मक विषम वितरण वक्र के दाईं ओर आते हैं।

नीचे दिए गए चित्र पर एक नजर डालें: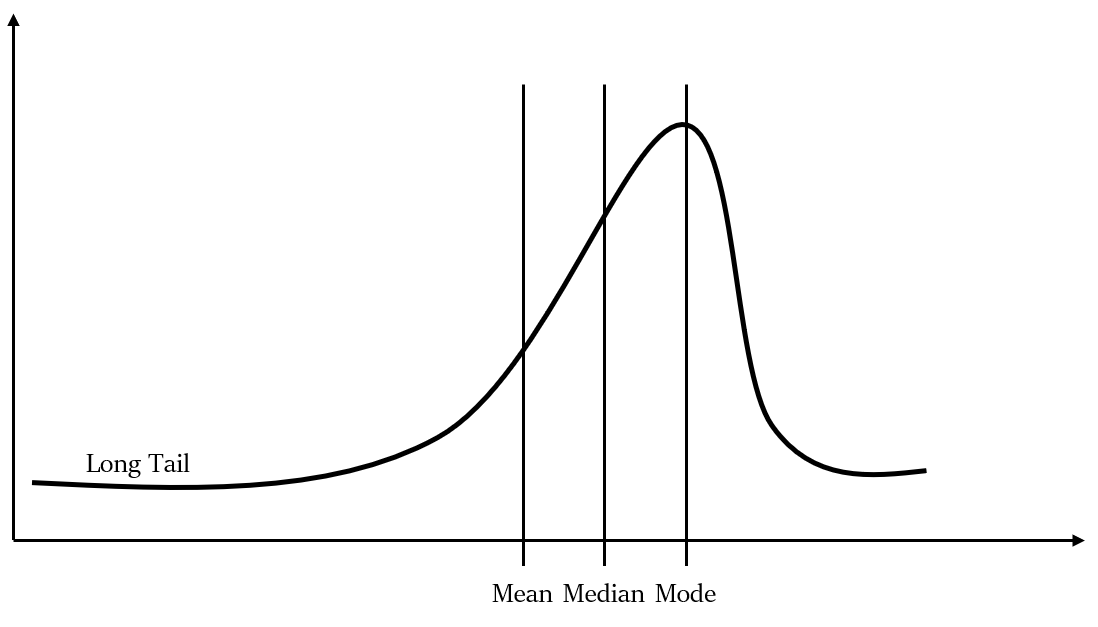
Statistics

Statistics

जैसा कि आप देख सकते हैं, यहाँ माध्य और माध्यिका दोनों बहुलक से कम हैं, और सामान्य तौर पर, माध्य भी माध्यिका से कम होता है। यानी माध्य < माध्यिका < बहुलक

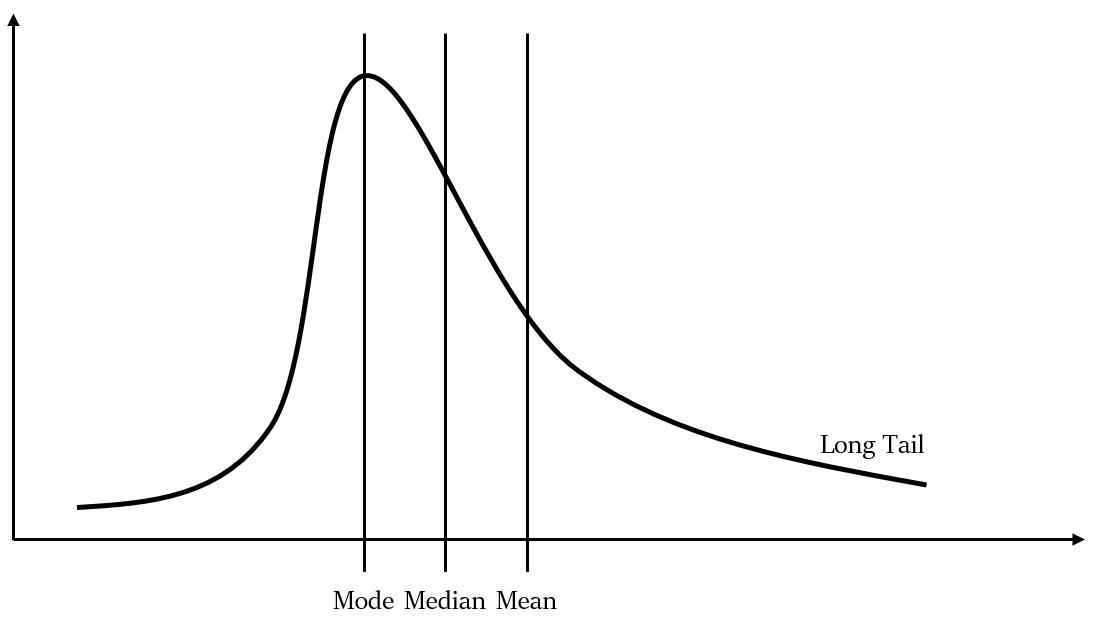
दायाँ विषम वितरण (Right skewed distribution)

दायाँ विषम वितरण को सकारात्मक विषम वितरण के रूप में भी जाना जाता है।

दाएं-विषम वितरण में एक लंबी दाहिनी पूंछ होती है, यानी संख्या रेखा पर सकारात्मक दिशा में लंबी पूंछ होती है। बाईं पूंछ छोटी होती है।

यह विषम वितरण इसलिए होता है क्योंकि अधिकांश डेटा मान सकारात्मक विषम वितरण वक्र के बाईं ओर आते हैं।

नीचे दिए गए चित्र पर एक नजर डालें:
Statistics

Statistics

जैसा कि आप देख सकते हैं, यहाँ माध्य और माध्यिका दोनों बहुलक से बड़े हैं, और सामान्य तौर पर, माध्य भी माध्यिका से बड़ा होता है। यानी माध्य > माध्यिका > बहुलक

नोट

आपका पाला सकारात्मक विषम वितरण से अधिक पड़ेगा, क्योंकि वे नकारात्मक विषम वितरण की तुलना में अधिक सामान्य होते हैं।

पियर्सन के विषमता गुणांक (Pearson's Coefficient of Skewness)

Pearson's Coefficient of Skewness का उपयोग यह निर्धारित करने के लिए किया जाता है कि वितरण सकारात्मक रूप से तिरछा/विषम है या नकारात्मक रूप से तिरछा/विषम है।

Pearson's Coefficient of Skewness = $\frac{माध्य \hspace{1ex} - \hspace{1ex} बहुलक}{Standard \hspace{1ex} deviation}$

यदि पियर्सन के विषमता गुणांक का मान :

शून्य है - इसका मतलब बिल्कुल भी विषमता नहीं है, यानी सामान्य वितरण (Normal distribution)
ऋणात्मक है - इसका अर्थ है कि वितरण नकारात्मक रूप से विषम है - एक कारण है जिसकी वजह से इस तरह के वितरण को ऋणात्मक विषम वितरण कहा जाता है। ऐसा इसलिए है, क्योंकि ऋणात्मक विषम वितरण में माध्य < बहुलक होता है।
सकारात्मक है - इसका मतलब है कि वितरण सकारात्मक रूप से विषम है - एक कारण है जिसकी वजह से इस तरह के वितरण को सकारात्मक विषम वितरण कहा जाता है। ऐसा इसलिए है, क्योंकि धनात्मक विषम वितरण में माध्य > बहुलक होता है।