वेन आरेख क्या हैं? (Venn Diagrams kya hote hein ?)

Overview

इस लेख में हम रीजनिंग के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Venn Diagrams, in Hindi

इस लेख में, हम यह समझने जा रहे हैं कि वेन डायग्राम (Venn Diagrams) क्या हैं, और इस विषय पर आम तौर पर किस तरह के reasoning प्रश्न पूछे जाते हैं।

वेन आरेख (Venn Diagram) - यह गणितीय या तार्किक समुच्चयों (mathematical or logical sets) को वृत्तों (circles) या अन्य बंद वक्रों (closed curves) के रूप में चित्रित करने वाला एक आरेख होता है| कभी-कभी इनको सार्वभौमिक समुच्चय (universal set) का प्रतिनिधित्व करने वाले आयत के भीतर दिखाया जाता है।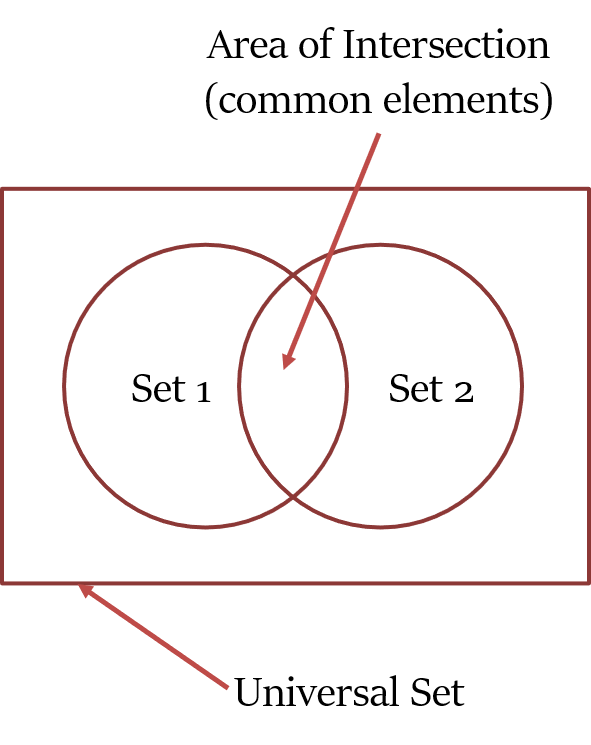

Venn diagrams

विभिन्न प्रकार के वेन आरेख प्रश्न:

• संबंध आधारित वेन आरेख (Relation based Venn diagrams)

• विश्लेषण आधारित वेन आरेख (Analysis based Venn diagrams)

आइये, इन दोनों प्रकार के प्रश्नों को गहरायी से समझते हैं|

संबंध आधारित वेन आरेख (Relation based Venn diagrams)

इस विषय पर प्रश्न, दी गयी चीज़ों के बीच संबंध खोजने, और उसे आरेखीय रूप से चित्रित करने की उम्मीदवार की क्षमता की जांच करते हैं।

तो आइए जानें कि किसी दिए गए संबंध को वेन आरेख के रूप में कैसे निरूपित किया जाए।

सामान्य तौर पर आपका सामना इन 10 प्रकार के संबंधों में से किसी से भी हो सकता है।

संबंध प्रकार 1

एक वर्ग (या सेट) पूरी तरह से दूसरे वर्ग से संबंधित है।

उदाहरण के लिए, राजस्थान भारत के अंदर एक राज्य है।

Venn diagrams

संबंध प्रकार 2

दिए गए वर्गों (या सेट) के बीच कोई संबंध नहीं है, अर्थात कोई भी तत्व समान नहीं है।

उदाहरण के लिए, भारत और फ्रांस दो अलग-अलग देश हैं।

Venn diagrams

संबंध प्रकार 3

एक वर्ग, दूसरे वर्ग से आंशिक रूप से संबंधित है, यानी उनमें कुछ तत्व समान हैं।

उदाहरण के लिए, भारत में कुछ हिंदू हैं।

Venn diagrams

आइए एक और उदाहरण पर विचार करें:

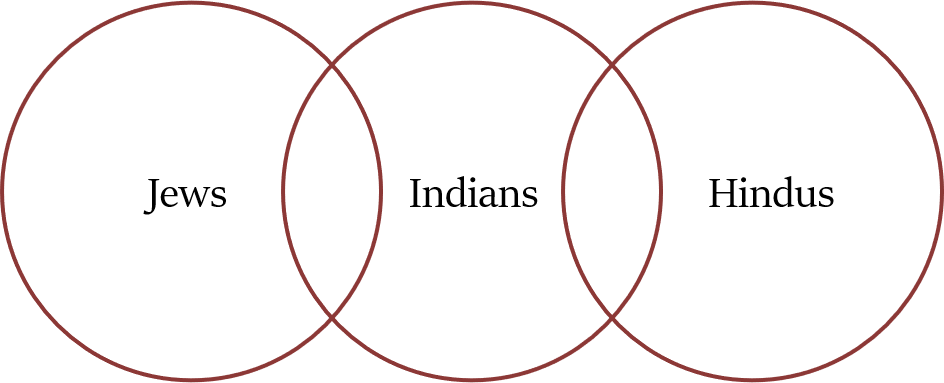
Venn diagrams

यदि तीनों सेटों के बीच ओवरलैप हो, तो हमें अगला संबंध प्रकार मिलता है।

संबंध प्रकार 4

तीनों अलग-अलग वर्ग आंशिक रूप से एक दूसरे से संबंधित हैं।

उदाहरण के लिए, भारतीयों, वैज्ञानिकों और शिक्षकों के सेट।

Venn diagrams

• कुछ भारतीय वैज्ञानिक हैं, कुछ नहीं हैं। इसी तरह, कुछ वैज्ञानिक भारतीय हैं, कुछ नहीं हैं।
• कुछ भारतीय शिक्षक हैं, कुछ नहीं हैं। इसी तरह, कुछ शिक्षक भारतीय हैं, कुछ नहीं हैं।
• कुछ शिक्षक वैज्ञानिक हैं, कुछ नहीं हैं। इसी तरह, कुछ वैज्ञानिक शिक्षक हैं, कुछ नहीं हैं।

संबंध प्रकार 5

दो वर्ग आंशिक रूप से एक दूसरे से संबंधित हैं और तीसरा वर्ग इन दोनों से पूरी तरह अलग है।

उदाहरण के लिए, वकीलों, प्रोफेसरों और बंदरों के सेट।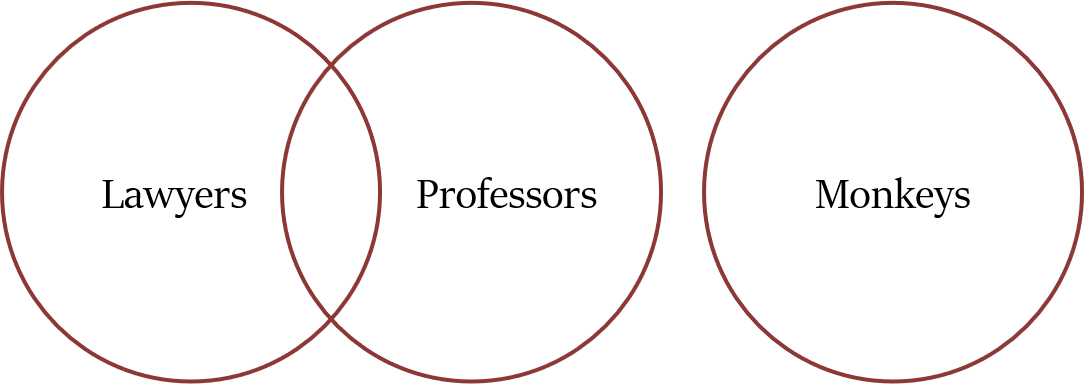

Venn diagrams

• कुछ वकील प्रोफेसर हैं, कुछ नहीं हैं। इसी तरह, कुछ प्रोफेसर वकील हैं, कुछ नहीं हैं।
• लेकिन कोई बंदर, वकील या प्रोफेसर नहीं हो सकता।

संबंध प्रकार 6

एक वर्ग पूरी तरह से दूसरे वर्ग के अंदर है, जबकि तीसरा वर्ग दोनों से पूरी तरह अलग है।

उदाहरण के लिए, कैलिफ़ोर्निया, U.S.A. और जर्मनी के सेट।

Venn diagrams

• कैलिफोर्निया पूरी तरह से U.S.A. के भीतर का एक राज्य है।
• जर्मनी, U.S.A. से अलग देश है।

संबंध प्रकार 7

एक वर्ग पूरी तरह से दूसरे वर्ग के अंदर है, और तीसरा वर्ग आंशिक रूप से द्वितीय वर्ग से संबंधित है।

उदाहरण के लिए, शाकाहारी, मांसाहारी और गायों के वर्ग।

Venn diagrams

• कुछ शाकाहारी मांसाहारी हो सकते हैं और इसके विपरीत भी सही है (जैसे भालू)। तो, प्रतिच्छेदन (overlap) का क्षेत्र सर्वाहारी (Omnivores) जानवरों को दर्शाता है।
• सभी गाय शुद्ध शाकाहारी (Herbivores) हैं।

संबंध प्रकार 8

एक वर्ग पूरी तरह से दूसरे वर्ग के अंदर है, और तीसरा वर्ग आंशिक रूप से इन दोनों से संबंधित है।

उदाहरण के लिए, पुरुषों, भाइयों और इंजीनियरों के सेट।

Venn diagrams

• सभी भाई पुरुष हैं।
• कुछ पुरुष इंजीनियर हैं, और कुछ इंजीनियर पुरुष हैं।
• कुछ भाई इंजीनियर हैं और कुछ इंजीनियर भाई हैं।

संबंध प्रकार 9

दो अलग-अलग वर्ग पूरी तरह से तीसरे वर्ग के अंदर हैं।

उदाहरण के लिए, तत्वों (Elements), तांबे (Copper) और सोने (Gold) के वर्ग।

Venn diagrams

• तांबा और सोना दोनों तत्व हैं।
• कोई तांबा, सोना नहीं है और कोई सोना, तांबा नहीं है।

संबंध प्रकार 10

दो वर्ग तीसरे वर्ग से इस प्रकार संबंधित हैं, कि इन दोनों वर्गों में से प्रत्येक की कुछ चीज़ें उस तीसरे वर्ग के समान हैं।

उदाहरण के लिए, मांसाहारी, शाकाहारी और पशु वर्ग।

Venn diagrams

• कुछ मांसाहारी शाकाहारी हैं, और कुछ शाकाहारी मांसाहारी हैं।
• मांसाहारी और शाकाहारी दोनों ही पशु हैं।

विश्लेषण आधारित वेन आरेख (Analysis based Venn diagrams)

इस प्रकार के प्रश्नों में आम तौर पर विभिन्न ज्यामितीय आकृतियों से युक्त एक वेन आरेख दिया जाता है। आरेख में प्रत्येक ज्यामितीय आकृति एक निश्चित वर्ग (अर्थार्थ सेट) का प्रतिनिधित्व करती है। उम्मीदवार को वेन आरेख का ध्यानपूर्वक अध्ययन और विश्लेषण करने, और फिर उसके आधार पर दिए गए प्रश्नों के उत्तर देने की आवश्यकता होती है।

ऐसे प्रश्नों को हल करने के लिए, एक छात्र को इन छह अवधारणात्मक शब्दों की ठोस समझ होनी चाहिए:

1. और (AND) - यह सर्वनिष्ठ, intersection है (A Ո B)
2. या (OR) - यह सम्मिलन, union है (A U B)
3. केवल (Only)
4. नहीं (Not)
5. कम से कम (At least)
6. अधिक से अधिक (At most)

आइए, कुछ उदाहरणों का उपयोग करके इन्हें समझते हैं।

आइए एक ऐसे परिदृश्य पर विचार करें, जहां हमारे पास तीन भाषाओं - अंग्रेजी, संस्कृत और जर्मन में से एक या अधिक बोलने वाले लोग हों।

वेन आरेख:

Venn diagrams

प्र. निम्न आंकड़ा दो प्रमुख समाचार चैनलों के दर्शकों की संख्या को दर्शाता है। उन लोगों की संख्या ज्ञात कीजिए, जो कोई समाचार चैनल नहीं देखते हैं।

वेन आरेख:

Venn diagrams

(a) 175   (b) 75   (c) 195   (d) 135 

स्पष्टीकरण :
1 2