त्रिभुज के क्षेत्रफल से सम्बंधित सूत्र और गुण (Formulae and Properties of Area of a Triangle)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Formulae and Properties of Area of a Triangle, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• ज्यामिति क्या होती है?
• ज्यामिति में रेखाएं और कोण
• ज्यामिति में त्रिभुज
• त्रिभुज से संबंधित महत्वपूर्ण रेखाएं और बिंदु
• त्रिभुज से सम्बंधित महत्वपूर्ण प्रमेय और नियम
• समरूपता प्रमेय और उनके अनुप्रयोग
• त्रिभुजों की सर्वांगसमता और समरूपता क्या होती हैं?
• त्रिभुज के क्षेत्रफल से सम्बंधित सूत्र और गुण
• चतुर्भुज और उसके गुण
• चतुर्भुज के क्षेत्रफल से सम्बंधित सूत्र और गुण
• समांतर चतुर्भुज और उसके गुण
• समलंब चतुर्भुज और उसके गुण
• बहुभुज और उसके गुण
• वृत्त और उसके गुण
• वृत्त प्रमेय

इस लेख में, हम त्रिभुज के क्षेत्रफल से संबंधित विभिन्न अवधारणाओं के बारे में जानेंगे, और विभिन्न सूत्रों के बारे में भी जिनका उपयोग हम इसे खोजने के लिए कर सकते हैं।

क्षेत्रफल क्या होता है? (What is Area?)

एक समतल आकृति का क्षेत्रफल उसकी सीमा रेखाओं के भीतर संलग्न सतह की मात्रा है। इसे वर्ग इकाइयों में व्यक्त किया जाता है, जैसे की वर्ग मीटर, वर्ग सेंटीमीटर, वर्ग इंच, आदि।

त्रिभुज के मामले में, यह उसकी तीन सीमा रेखाओं के भीतर संलग्न सतह की मात्रा है।

परिधि क्या होती है? (What is Perimeter?)

एक समतल आकृति का परिमाप उसकी भुजाओं की कुल लंबाई है।

त्रिभुज के मामले में, यह इसकी तीन भुजाओं की कुल लंबाई है।

त्रिभुज के क्षेत्रफल से संबंधित सूत्र (Formulae ralated to Area of a Triangle)

त्रिभुज का क्षेत्रफल ज्ञात करने के लिए विभिन्न सूत्र हैं। उनमें से कुछ को किसी भी त्रिभुज पर लागू किया जा सकता है, जबकि अन्य केवल एक निश्चित प्रकार के त्रिभुज पर लागू होते हैं। आइए, उनमें से कुछ को देखें।

किसी भी त्रिभुज का क्षेत्रफल ज्ञात करने के सूत्र (Formulae for finding area of any Triangle)

अगर आधार और ऊंचाई ज्ञात हो (If base and height are known)

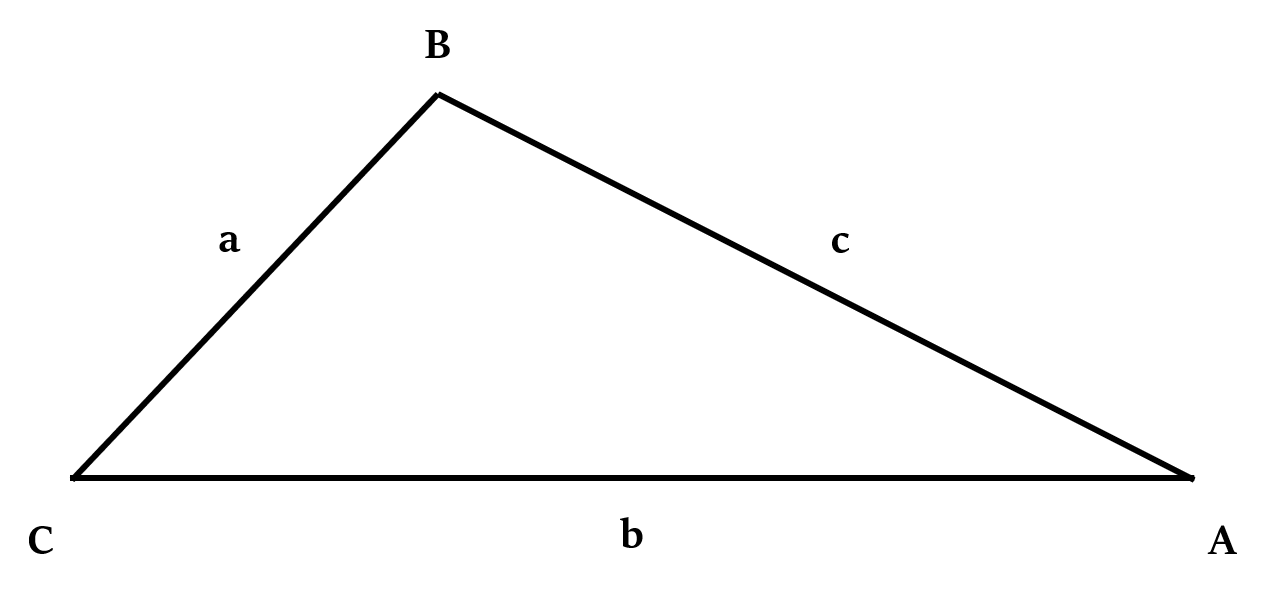
यदि त्रिभुज की एक भुजा की लंबाई, जो कि आधार है, b है। और त्रिभुज की ऊँचाई h है, तो: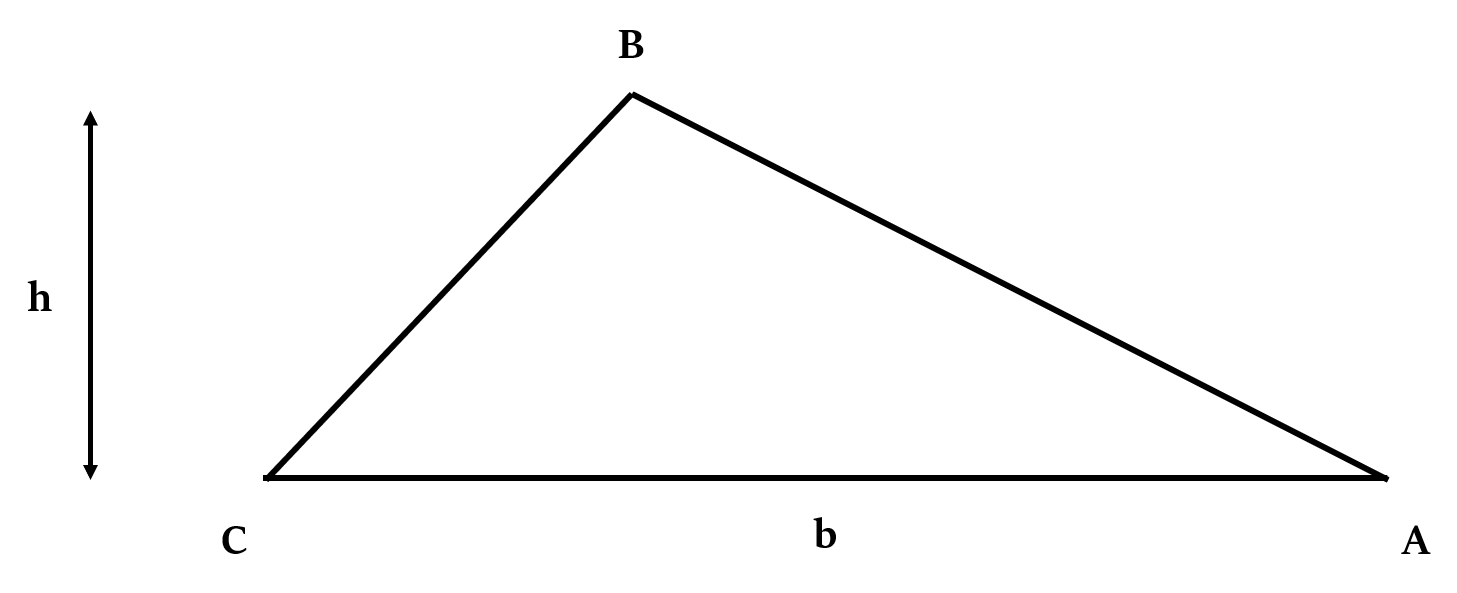

Geometry

त्रिभुज का क्षेत्रफल = $\frac{1}{2}$ × आधार × ऊँचाई = $\frac{1}{2}$ × b × h

नोट

मापी गई ऊँचाई (h), आधार (b) के लंबवत होनी चाहिए।

एक समकोण त्रिभुज के मामले में, इसकी दो भुजाएँ पहले से ही एक दूसरे के लंबवत होती हैं (कर्ण के अलावा)। तो, इसका क्षेत्रफल = $\frac{1}{2}$ × समकोण वाली भुजाओं का गुणनफल

यदि तीनों भुजाएँ ज्ञात हों (Heron's formula)

यदि किसी त्रिभुज की तीनों भुजाओं की लंबाई ज्ञात हो, मान लीजिए a, b और c, तो:

Geometry

त्रिभुज का क्षेत्रफल = $\sqrt{s (s - a) (s - b) (s - c)}$, जहाँ s = $\frac{a + b + c}{2}$

नोट

s त्रिभुज की अर्ध-परिधि (semi-perimeter) है।

यदि तीनों माध्यिकाएं ज्ञात हों (If all the three medians are known)

यदि किसी त्रिभुज की तीनों माध्यिकाओं की लंबाई ज्ञात हो, मान लीजिए p, q और r, तो: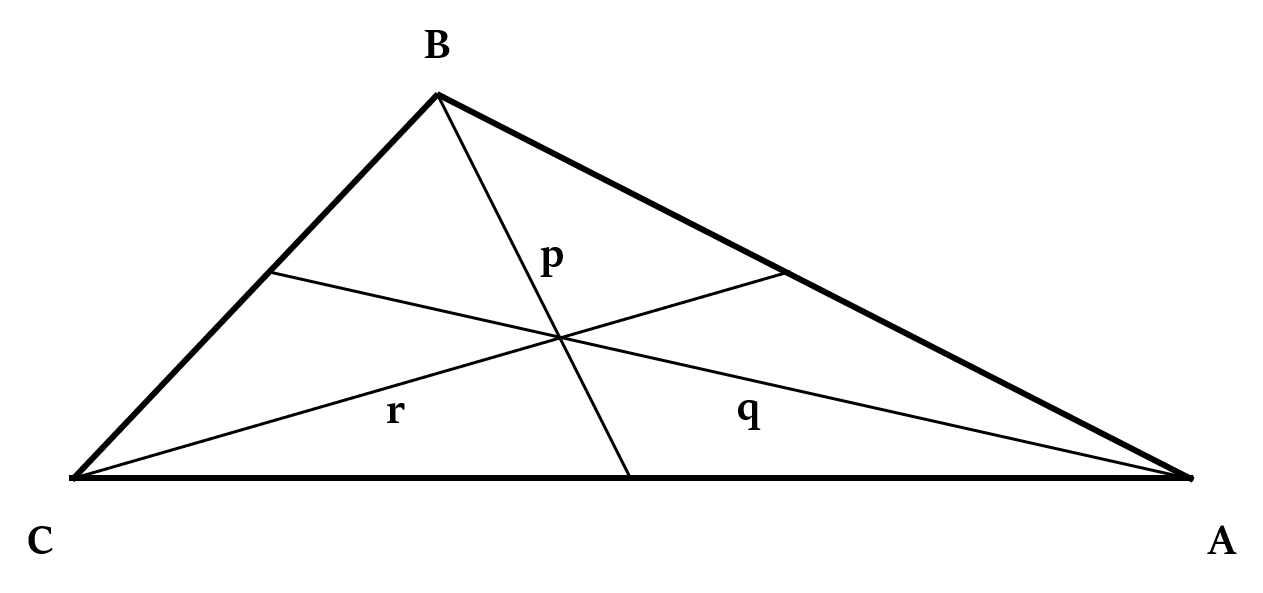

Geometry

त्रिभुज का क्षेत्रफल = $\frac{4}{3} \sqrt{z (z - p) (z - q) (z - r)}$, जहाँ z = $\frac{p + q + r}{2}$

समबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के सूत्र (Formulae for finding area of Equilateral Triangle)

हम एक समबाहु त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं, यदि इसकी भुजा या ऊँचाई दी गई हो।

मान लीजिए कि एक समबाहु त्रिभुज की एक भुजा की लंबाई a है, और इसकी ऊँचाई h है।

नोट

सबसे पहले, आइए हम एक समबाहु त्रिभुज की भुजा और ऊँचाई के बीच संबंध को जानें।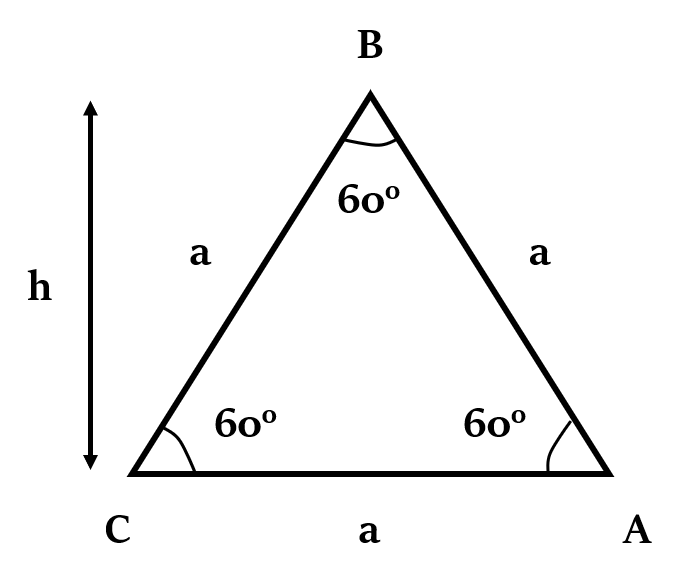

Geometry

एक समबाहु त्रिभुज की ऊँचाई, h = $\frac{\sqrt{3}}{2}$ × a
या समबाहु त्रिभुज की किसी भी भुजा की लंबाई, a = $\frac{2}{\sqrt{3}}$ × h
(इसलिए, समबाहु त्रिभुज में, भुजा : ऊँचाई = 2 : $\sqrt{3}$ )

समबाहु त्रिभुज का क्षेत्रफल = $\frac{\sqrt{3}}{4} × a^2$

या समबाहु त्रिभुज का क्षेत्रफल = $\frac{h^2}{\sqrt{3}}$

समद्विबाहु त्रिभुज का क्षेत्रफल ज्ञात करने के सूत्र (Formulae for finding area of Isosceles Triangle)

एक समद्विबाहु त्रिभुज में, दो भुजाएँ बराबर होती हैं।

मान लीजिए कि दो समान भुजाएँ लंबाई b की हैं, और तीसरी भुजा की लंबाई a है।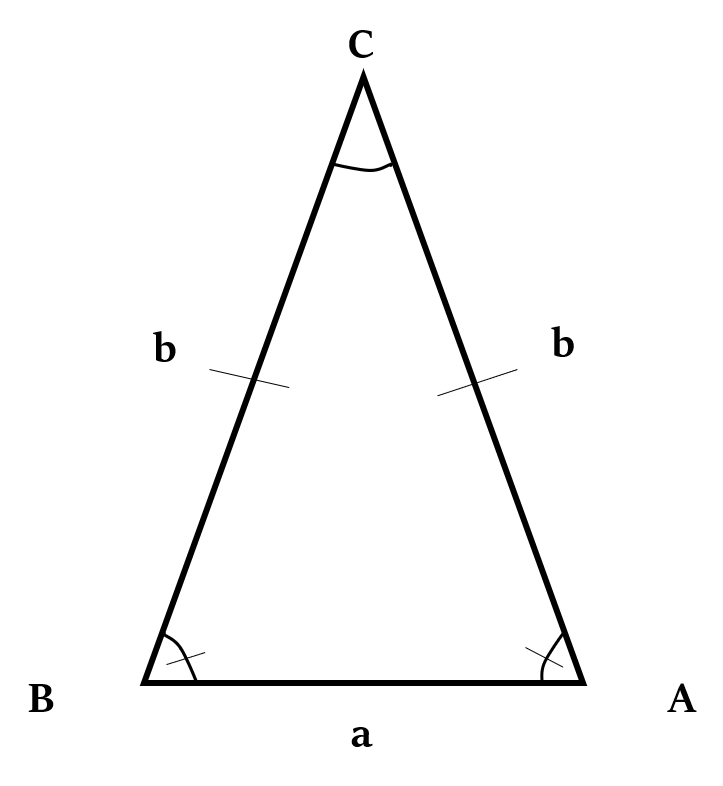

Geometry

समद्विबाहु त्रिभुज का क्षेत्रफल = $\frac{a}{4} \sqrt{4b^2 - a^2}$

नोट

समद्विबाहु त्रिभुज की ऊँचाई = $\frac{1}{2} \sqrt{4b^2 - a^2}$

त्रिभुज के क्षेत्रफल से संबंधित गुण (Properties ralated to Area of a Triangle)

गुण 1

यदि हम किसी त्रिभुज की भुजाओं के मध्य बिंदुओं को मिला दें, तो हमें चार सर्वांगसम (congruent) त्रिभुज प्राप्त होते हैं, जिनमें से प्रत्येक बड़े त्रिभुज के समरूप (similar) होता है।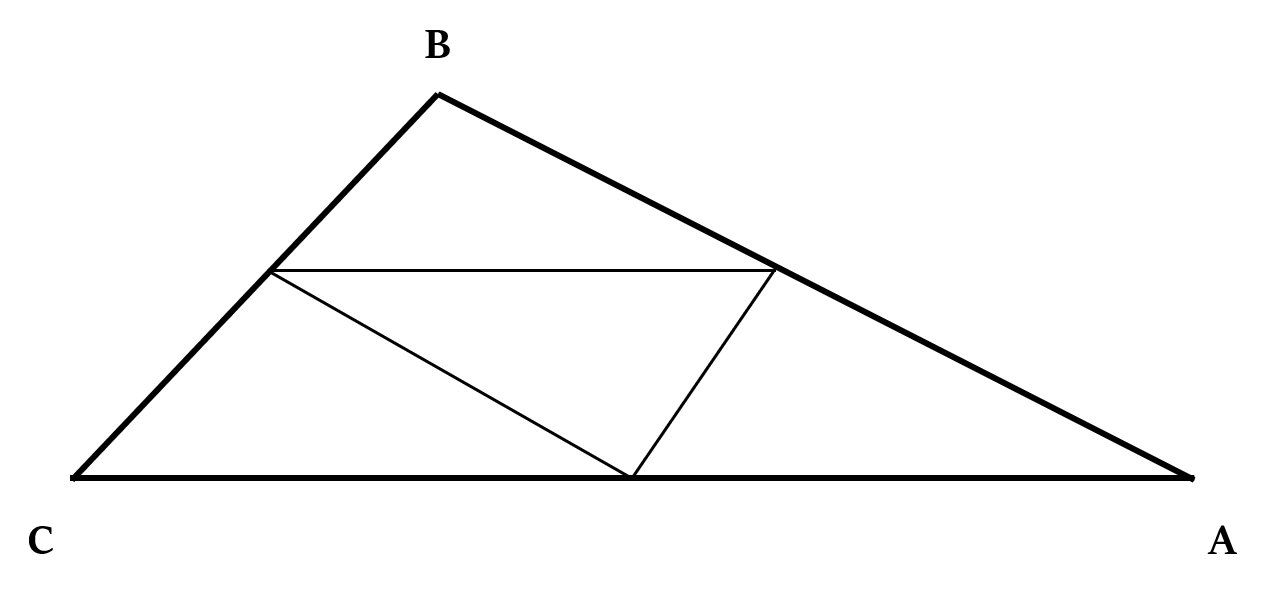

Geometry

इन छोटे त्रिभुजों (भुजाओं के मध्य-बिंदुओं को मिलाकर निर्मित) में से प्रत्येक का क्षेत्रफल = $\frac{1}{4}$ × मूल त्रिभुज का क्षेत्रफल

गुण 2

यदि दो त्रिभुजों का आधार समान है (या आधार समान लंबाई के हैं), और वे समान समानांतर रेखाओं के बीच हैं (अर्थात उनकी ऊँचाई समान है), तो उनका क्षेत्रफल समान होगा।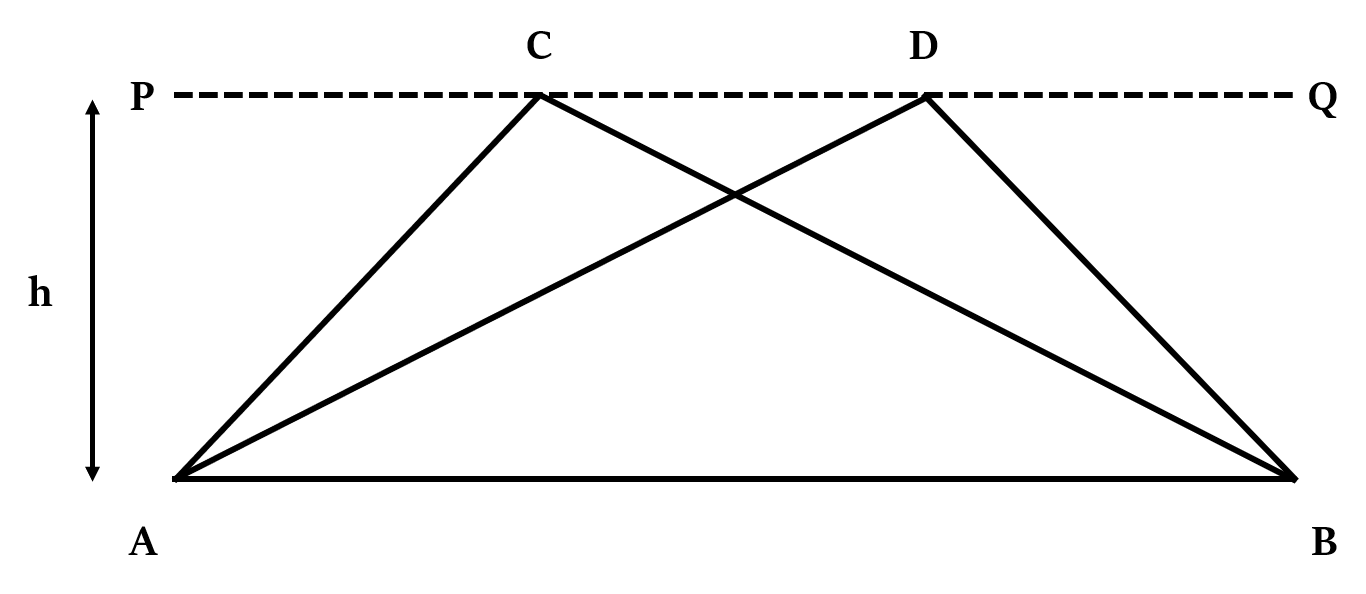

Geometry

इसका कारण यह है कि त्रिभुज का क्षेत्रफल उसके आधार और ऊँचाई के गुणनफल का आधा होता है। यदि दो त्रिभुजों की ऊँचाइयाँ समान हैं और उनके आधारों की लंबाई भी (जैसा कि ऊपर है), तो स्पष्ट रूप से उनका क्षेत्रफल समान होगा।

नोट

यदि एक त्रिभुज और एक समांतर चतुर्भुज (parallelogram) का आधार समान है (या उनके आधार समान लंबाई के हैं), और वे समान समानांतर रेखाओं के बीच हैं (अर्थात उनकी ऊँचाई समान है), तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होगा।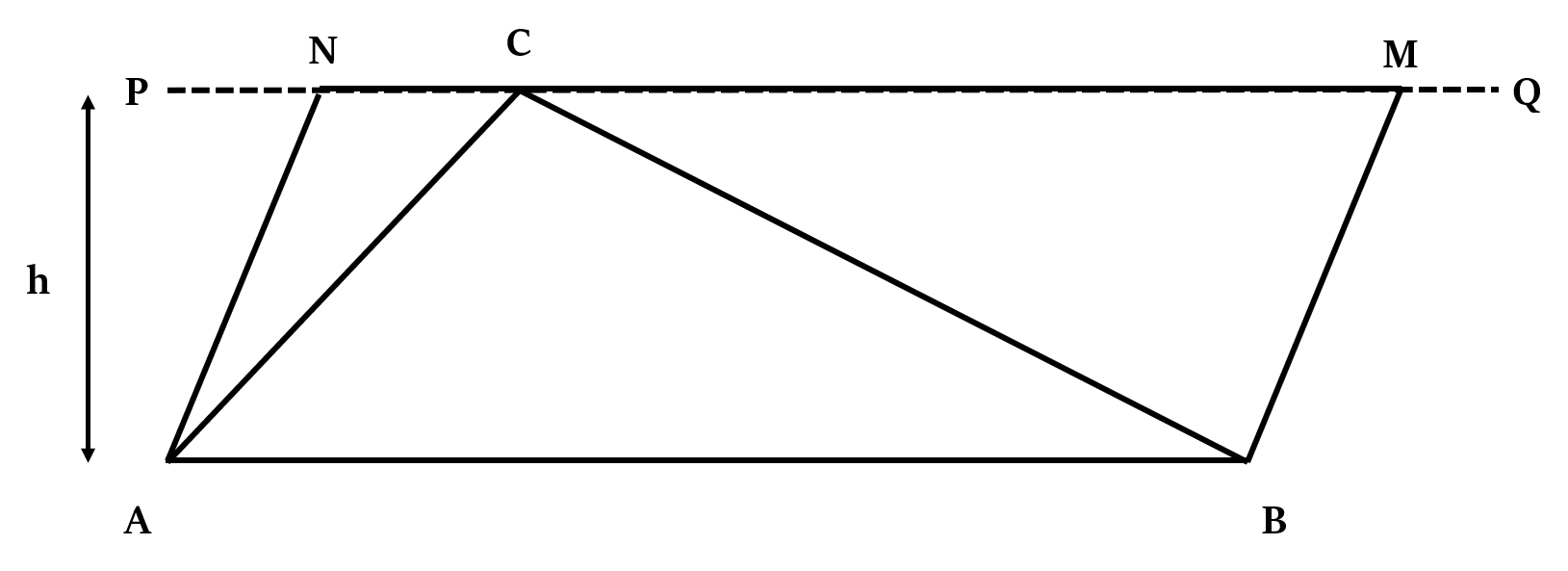

Geometry

यदि AB ∥ PQ, तो, ∆ABC का क्षेत्रफल = $\frac{1}{2}$ × समांतर चतुर्भुज ABMN का क्षेत्रफल

गुण 3

यदि हम किसी त्रिभुज के किसी शीर्ष से विपरीत भुजा पर एक रेखा डालते हैं, तो यह स्पष्ट रूप से मूल त्रिभुज को दो भागों में विभाजित करेगी, जैसा कि नीचे दिखाया गया है: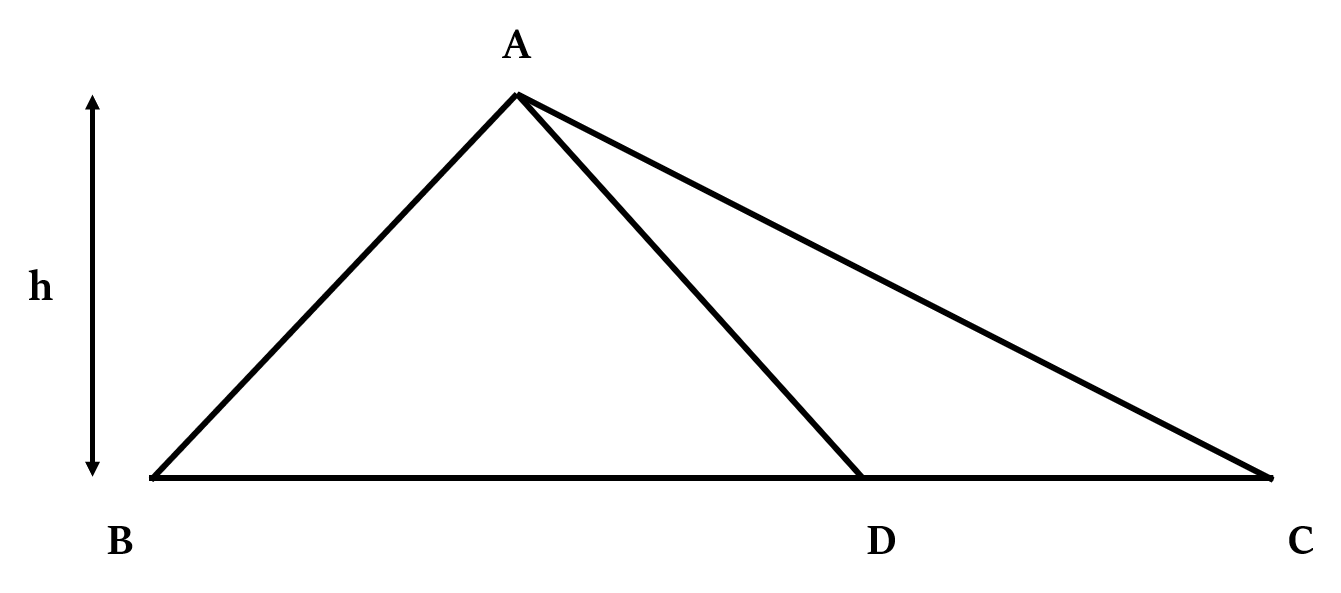

Geometry

इन दोनों त्रिभुजों के क्षेत्रफल का अनुपात उनके आधारों के अनुपात के बराबर होगा।

यानी, $\frac{∆ABD \hspace{1ex} का \hspace{1ex} क्षेत्रफल}{∆ADC \hspace{1ex} का \hspace{1ex} क्षेत्रफल} = \frac{BD}{DC}$

नोट

उदाहरण के लिए, एक त्रिभुज की माध्यिका (Median) उसे समान क्षेत्रफल वाले दो त्रिभुजों में विभाजित करेगी।

इसका कारण यह है कि त्रिभुज का क्षेत्रफल उसके आधार और ऊँचाई के गुणनफल का आधा होता है। यदि दो त्रिभुजों की ऊँचाइयाँ समान हैं (जैसा कि ऊपर है), तो उनका क्षेत्रफल उनके आधारों के अनुपात में ही होगा।

गुण 4: अधिकतम संभावित क्षेत्र (Maximum Possible Area)

गुण 4a

यदि आपको एक त्रिभुज का परिमाप (perimeter) दिया गया है, तो आप ऐसा कौन सा त्रिभुज बनाएंगे जिससे अधिकतम क्षेत्रफल (maximum possible area) संभव हो?

उत्तर समबाहु त्रिभुज (equilateral triangle) है।

दूसरे शब्दों में, यदि दो या दो से अधिक त्रिभुजों का परिमाप (perimeter) समान हो, तो समबाहु त्रिभुज का क्षेत्रफल अधिकतम होगा।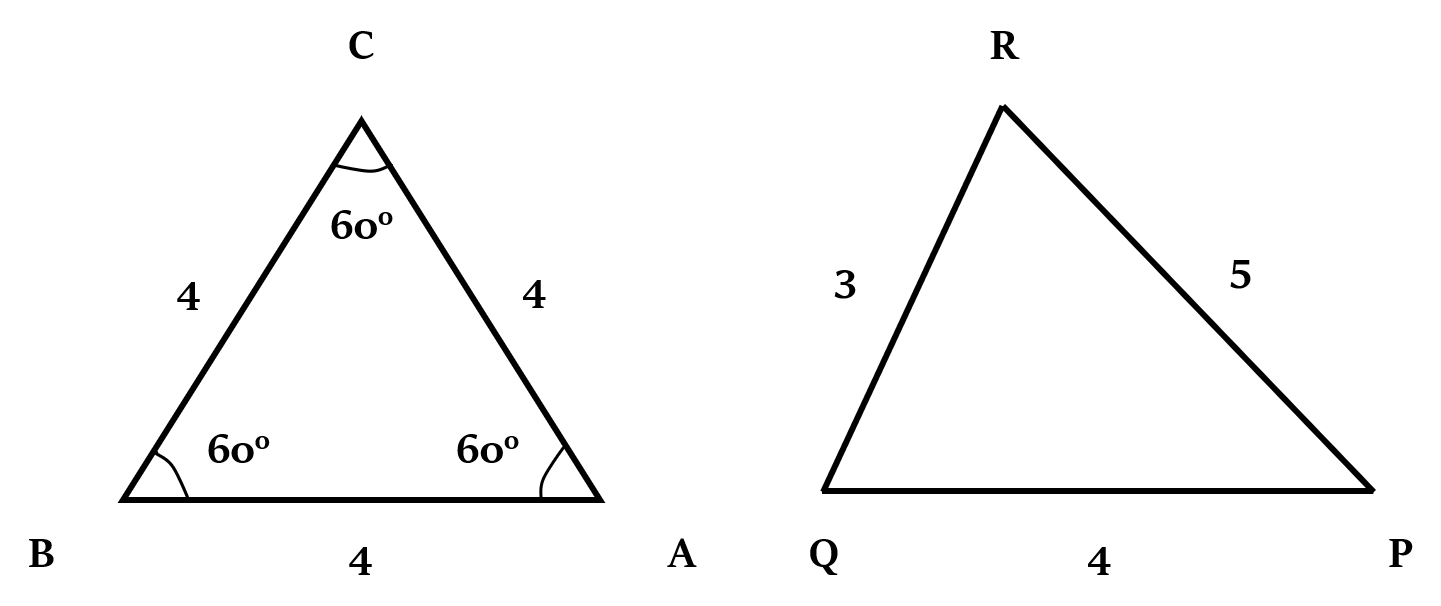

Geometry

गुण 4b

यदि आपको एक वृत्त दिया जाता है, तो आप उसके अंदर किस प्रकार का त्रिभुज बनाएंगे, जिससे अधिकतम क्षेत्रफल (maximum possible area) संभव हो?

उत्तर फिर से वही है - समबाहु त्रिभुज।

दूसरे शब्दों में, यदि एक वृत्त में दो या दो से अधिक त्रिभुज बने हुए हों, तो समबाहु त्रिभुज का क्षेत्रफल अधिकतम होगा।