समरूपता प्रमेय और उनके अनुप्रयोग (Similarity Theorems and their applications)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Similarity Theorems and their applications, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• ज्यामिति क्या होती है?
• ज्यामिति में रेखाएं और कोण
• ज्यामिति में त्रिभुज
• त्रिभुज से संबंधित महत्वपूर्ण रेखाएं और बिंदु
• त्रिभुज से सम्बंधित महत्वपूर्ण प्रमेय और नियम
• समरूपता प्रमेय और उनके अनुप्रयोग
• त्रिभुजों की सर्वांगसमता और समरूपता क्या होती हैं?
• त्रिभुज के क्षेत्रफल से सम्बंधित सूत्र और गुण
• चतुर्भुज और उसके गुण
• चतुर्भुज के क्षेत्रफल से सम्बंधित सूत्र और गुण
• समांतर चतुर्भुज और उसके गुण
• समलंब चतुर्भुज और उसके गुण
• बहुभुज और उसके गुण
• वृत्त और उसके गुण
• वृत्त प्रमेय

अब, जैसा कि हम पहले ही त्रिभुजों की समरूपता की अवधारणा को समझ चुके हैं, आइए इसके अनुप्रयोगों और इस पर आधारित कुछ प्रमेयों/अवधारणाओं को देखें।

प्रमेय 1: Thales theorem

थेल्स प्रमेय (Thales theorem) को मूल आनुपातिकता प्रमेय (Basic proportionality theorem) के रूप में भी जाना जाता है।

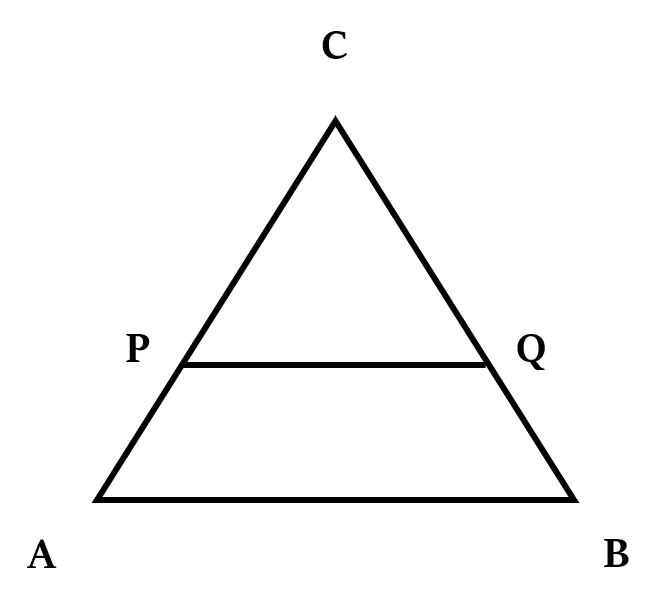
एक रेखा खंड, जो त्रिभुज की किसी भुजा के समानांतर होता है, उस त्रिभुज की अन्य दो भुजाओं को उसी अनुपात में काटता है, और यह मूल त्रिभुज के समरूप (similar) एक नया त्रिभुज बनाता है।

Geometry

उपरोक्त आकृति में, AB ∥ PQ.
क्यूंकि ∠C = ∠C, ∠A = ∠P, ∠B = ∠Q, इसलिए ∆ABC ~ ∆PQR

और क्यूंकि ∆ABC ~ ∆PQR, इसलिए $\frac{AB}{PQ} = \frac{BC}{QC} = \frac{AC}{PC}$

साथ ही, $\frac{AP}{PC} = \frac{BQ}{QC}$

$\frac{AC}{AP} = \frac{BC}{BQ}$

नोट

इसका उलटा भी सच है। यदि एक रेखाखंड त्रिभुज की दो भुजाओं को समान अनुपात में विभाजित करता है, तो यह रेखाखंड तीसरी भुजा के समानांतर होना चाहिए।

अर्थात्, यदि $\frac{AP}{PC} = \frac{BQ}{QC}$, तो इसका अर्थ है कि PQ ∥ AB

आइए, अब थेल्स प्रमेय के कुछ विशेष मामले और कुछ संबंधित नियमों को देखें।

Thales theorem का विशेष मामला

किसी त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड, उस त्रिभुज की तीसरी भुजा के समानांतर और उसकी लंबाई का आधा होता है।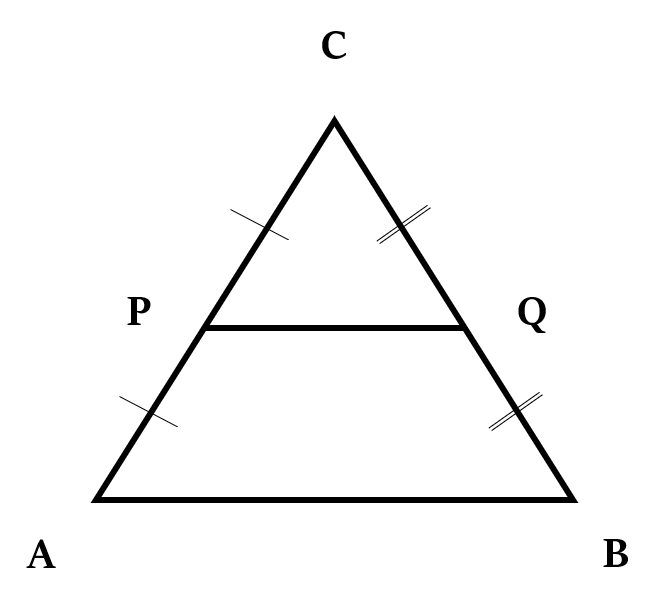

Geometry

यदि P और Q, AC और BC के मध्य-बिंदु हैं, तो PQ ∥ AB, और PQ = $\frac{1}{2}$ AB

अत: ∆PQC का क्षेत्रफल = $\frac{1}{4}$ ∆ABC

और, ∆PQC का क्षेत्रफल = $\frac{1}{3}$ □ABQP

नोट

दूसरे शब्दों में, यदि त्रिभुज की एक भुजा के समांतर रेखा दूसरी भुजा को समद्विभाजित करती है, तो वह तीसरी भुजा को भी समद्विभाजित करेगी।

यदि PQ ∥ AB और P, AC का मध्यबिंदु है, तो Q भी BC का मध्यबिंदु होगा।

संबंधित नियम (Related rule)

त्रिभुज की दो भुजाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखंड, शीर्ष को तीसरी भुजा से मिलाने वाली रेखा को भी समद्विभाजित करेगा।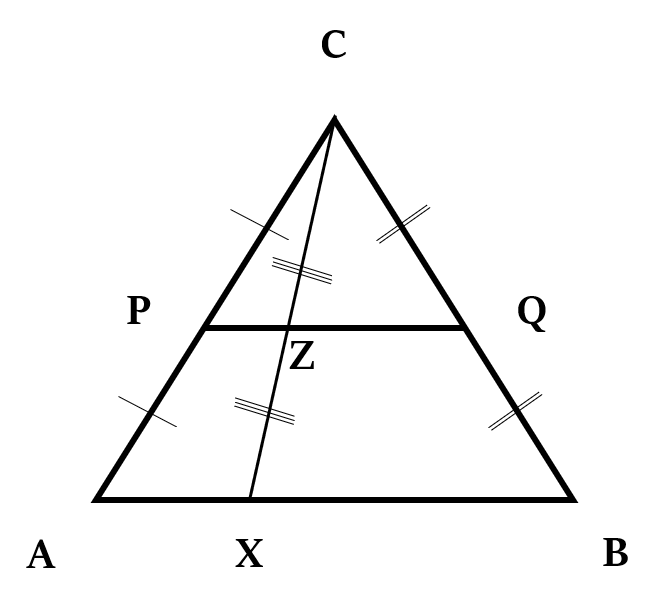

Geometry

उपरोक्त आकृति में, चूंकि P और Q क्रमशः AC और BC भुजाओं के मध्यबिंदु हैं, इसलिए CZ = XZ

प्रमेय 2

समकोण त्रिभुज में, समकोण के शीर्ष से कर्ण तक खींचा गया लंबवत त्रिभुज को दो भागों में विभाजित करता है, और एक दूसरे के समरूप (similar) और मूल त्रिभुज के समरूप (similar) दो छोटे त्रिभुज बनाता है।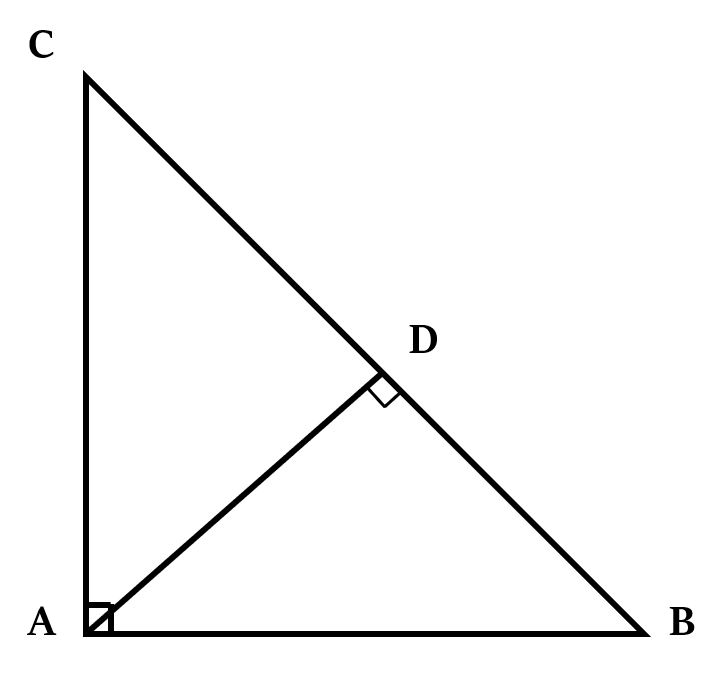

Geometry

उपरोक्त आकृति में, ∆ABC ~ ∆DAB ~ ∆DAC

• $AC^2$ = CB × CD ... (1)

• $AB^2$ = BC × BD ... (2)

• $AD^2$ = DC × DB ... (3)

इन तीनों से हम तीन और समीकरण बना सकते हैं।

समीकरण 1 और 2 का प्रयोग करते हुए, हम प्राप्त करते हैं:
$\frac{AC^2}{AB^2} = \frac{CD}{BD}$

समीकरण 2 और 3 का प्रयोग करते हुए, हम प्राप्त करते हैं:
$\frac{AB^2}{AD^2} = \frac{BC}{DC}$

समीकरण 1 और 3 का प्रयोग करते हुए, हम प्राप्त करते हैं:
$\frac{AC^2}{AD^2} = \frac{CB}{DB}$

• $\frac{1}{AD^2} = \frac{1}{AC^2} + \frac{1}{AB^2}$

या AD = $\frac{AC × AB}{BC}$

प्रमेय 3: समलंब चतुर्भुज से संबंधित (Related to Trapezium)

समलम्ब चतुर्भुज (AB ∥ CD) के विकर्ण, इसे चार त्रिभुजों में विभाजित करते हैं।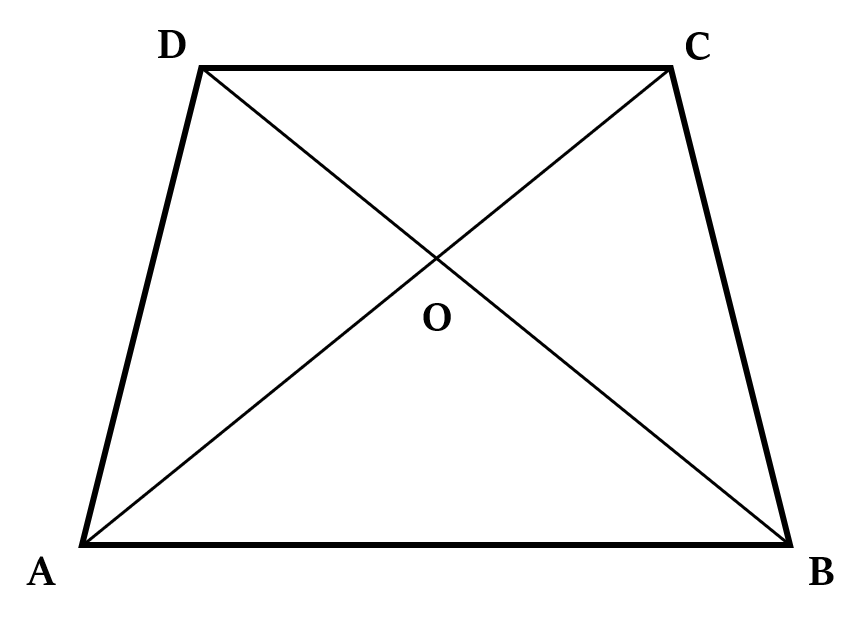

Geometry

• समांतर भुजा (parallel sides) के अनुदिश दो त्रिभुज समरूप (similar) हैं, अर्थात DOC ~ ∆AOB
• गैर-समानांतर भुजाओं (non-parallel sides) के अनुदिश दो त्रिभुज क्षेत्रफल में बराबर हैं, अर्थात ∆AOD का क्षेत्रफल = ∆BOC का क्षेत्रफल