सम्मिश्र संख्याओं का परिचय (Complex Numbers in Hindi)

Overview

इस लेख में, हम गणित के एक महत्वपूर्ण अध्याय - सम्मिश्र संख्याओं (Complex Numbers, कॉम्प्लेक्स नंबर्स), के मूल सिद्धांतों को समझने की कोशिश करेंगे।

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Complex Numbers, in Hindi

सम्मिश्र संख्या क्या हैं? (Complex Numbers kya hein?)

एक सम्मिश्र संख्या वास्तविक और काल्पनिक संख्याओं का एक संयोजन है। इसे इस प्रकार दर्शाया जाता है: a + ib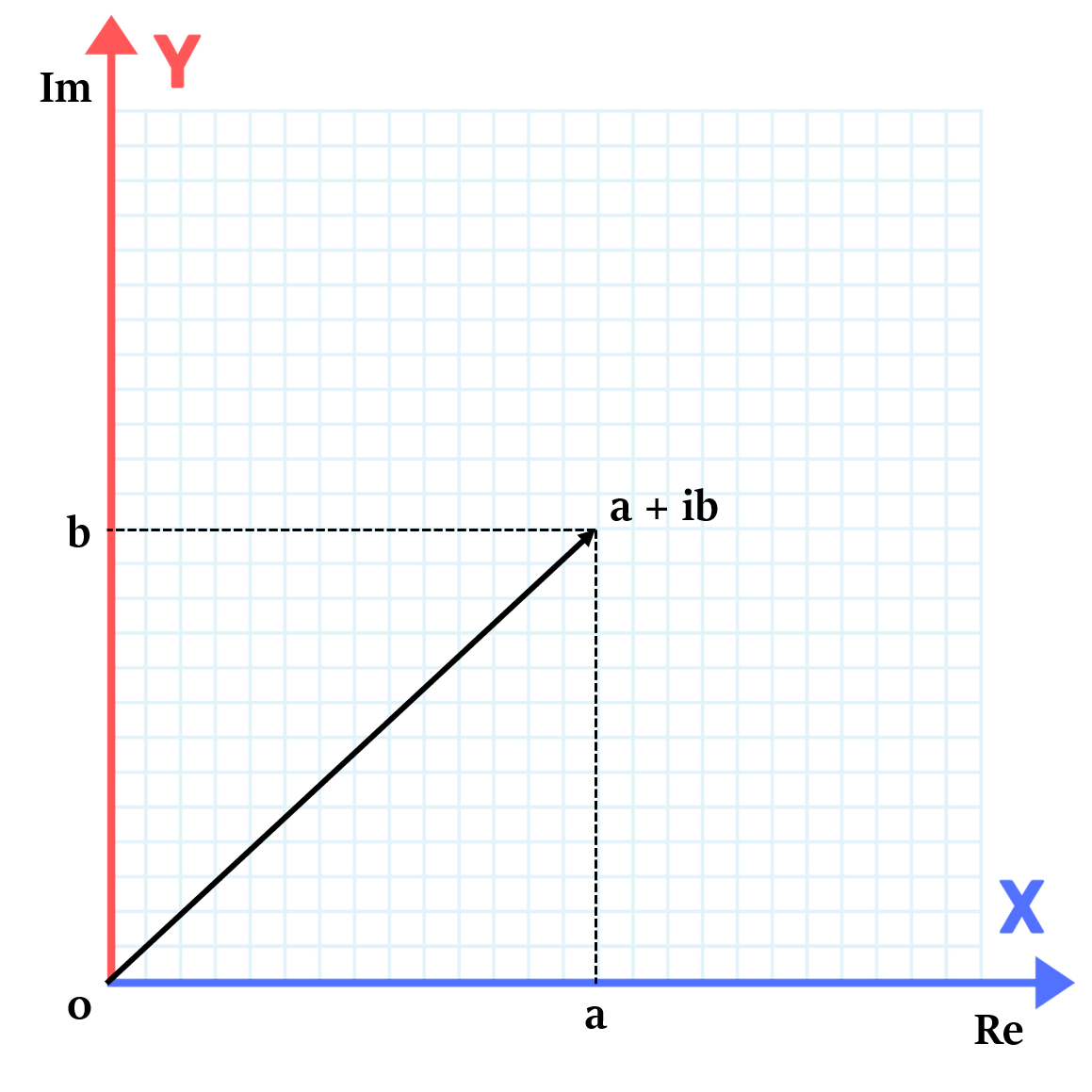

Complex Numbers

यहाँ 'a' और 'b' वास्तविक संख्याएँ हैं और 'i' (Iota) एक काल्पनिक संख्या है। i का मान -1 होता है।

इसलिए, यह समझने के लिए कि सम्मिश्र संख्याएँ क्या हैं, हमें वास्तविक संख्याओं और काल्पनिक संख्याओं को समझना चाहिए।

वास्तविक संख्याएँ (Re) वे संख्याएँ हैं जिनसे हम अपने दैनिक जीवन में दो-चार होते रहते हैं, जैसे की शून्य, धनात्मक संख्याएँ (1, 2, 5…), ऋणात्मक संख्याएँ (-1, -4, -134…), भिन्न (1/2, 3/5, 5/3…)। अर्थात्, वे सभी परिमेय और अपरिमेय संख्याओं (rational and irrational numbers) को अपने अंदर समाहित करते हैं। इन्हें एक संख्या रेखा पर निरूपित किया जा सकता है। किसी भी वास्तविक संख्या का वर्ग एक धनात्मक संख्या होती है।

इसके विपरीत, किसी संख्या रेखा पर काल्पनिक संख्याओं (Im) को प्रदर्शित नहीं किया जा सकता है। क्यों?

क्योंकि वे काल्पनिक हैं - उनका कोई मूर्त मूल्य नहीं है। कोई भी काल्पनिक संख्या किसी ऋणात्मक संख्या का वर्गमूल होती है, जैसे की √-3, √-5, आदि। दूसरे शब्दों में, यदि हम एक काल्पनिक संख्या का वर्ग करते हैं, तो परिणाम के रूप में हमें एक ऋणात्मक संख्या प्राप्त होगी।

एक सम्मिश्र संख्या, वास्तविक संख्याओं और काल्पनिक संख्याओं को मिलाकर बनती है, जैसे की 4 + √-5, 3 + √-2, आदि। हम इन्हें निम्न प्रकार से भी निरूपित कर सकते हैं:

• 4 + √-5 = 4 + i5
• 3 + √-2 = 3 + i2
• और इसी तरह आगे भी ...

नोट

वास्तविक संख्याएँ और काल्पनिक संख्याएँ भी सम्मिश्र संख्याएँ ही होती हैं।

• यदि सम्मिश्र संख्या a + ib में, b शून्य है, तो यह एक शुद्ध वास्तविक संख्या होगी। उदाहरण के लिए, 7 + 0i, -2 + 0i, आदि।
• यदि सम्मिश्र संख्या a + ib में, a शून्य है, तो यह एक शुद्ध काल्पनिक संख्या होगी। उदाहरण के लिए, 0 + 2i, 0 - 7i, आदि।
• शून्य भी एक सम्मिश्र संख्या है। इसे 0 + 0i के रूप में दर्शाया जा सकता है

सम्मिश्र संख्याओं के गुण

गुण 1

यदि a, और b वास्तविक संख्याएँ हैं और a + bi = 0 है, तो इसका अर्थ है कि:

• a = 0, और
• b = 0

गुण 2

यदि a, b, c, और d वास्तविक संख्याएँ हैं और a + bi = c + di, तो इसका अर्थ है कि:

• a = c, और
• b = d

सम्मिश्र संख्याओं का आरेखीय निरूपण

ग्राफ़ पर एक सम्मिश्र संख्या को निरूपित करने के लिए, हम वास्तविक संख्याओं को X-अक्ष (तथाकथित वास्तविक अक्ष) और काल्पनिक संख्याओं को Y-अक्ष (तथाकथित काल्पनिक अक्ष) पर रखते हैं।

उदाहरण के लिए, हम सम्मिश्र संख्या 2 + 4i को निम्नानुसार निरूपित कर सकते हैं: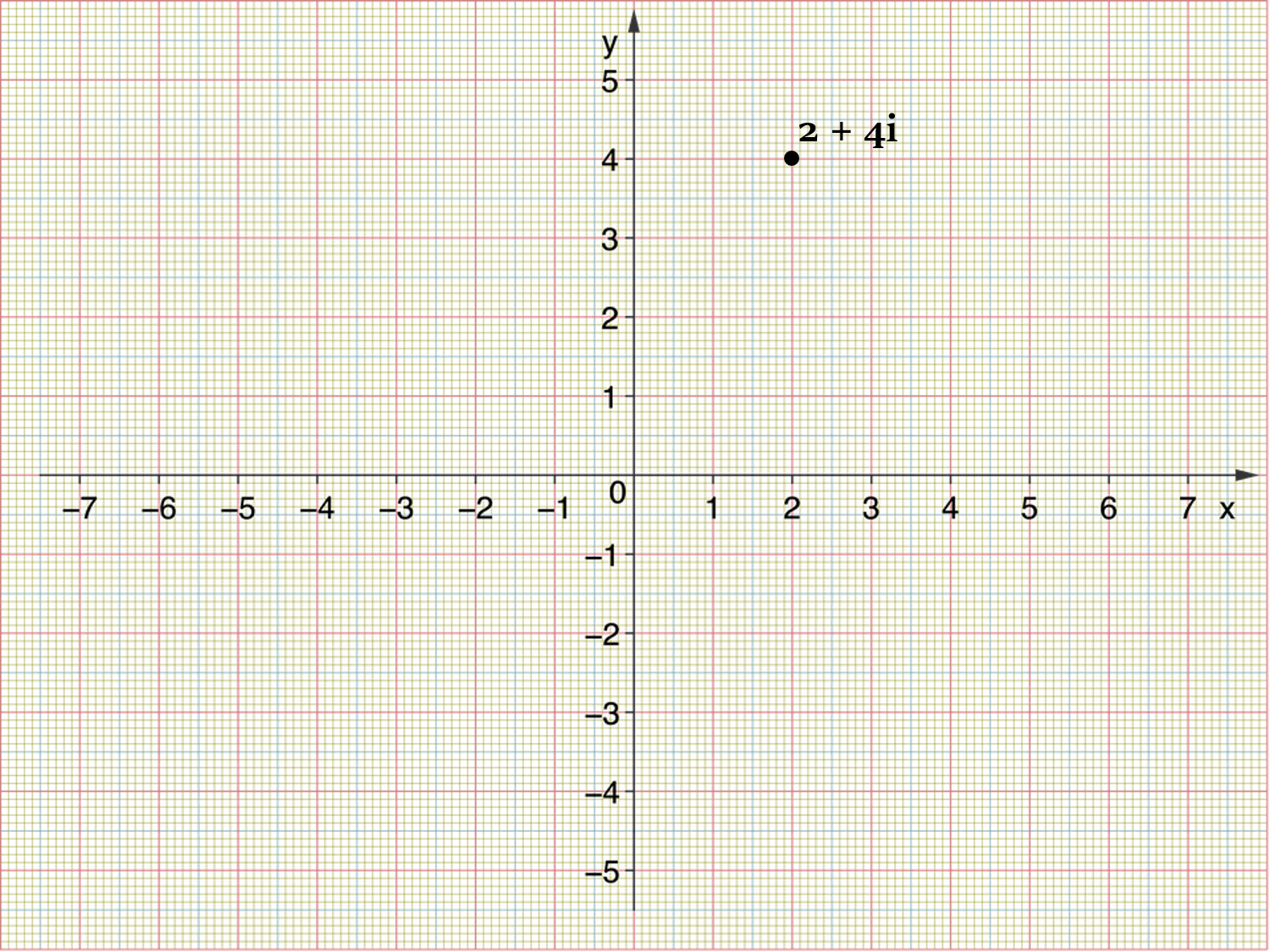

Complex Numbers

सम्मिश्र संख्याओं वाले तल को Argand (या सम्मिश्र) तल कहते हैं।

नोट

सामान्य निर्देशांक बिंदुओं (coordinate points) की तरह, हम सम्मिश्र संख्याओं को ध्रुवीय रूप (polar form) में भी निरूपित कर सकते हैं।

ध्रुवीय रूप में, सम्मिश्र संख्या को r और θ के रूप में दर्शाया जाता है। यहाँ, r उस सदिश की लंबाई है जो मूल (origin) से सम्मिश्र संख्या के बिंदु को जोड़ता है, और θ ऐसे सदिश द्वारा वास्तविक अक्ष के साथ बनाया गया कोण है।

आयोटा (i) के घातांक - Power of Iota

हम पहले से ही जानते हैं कि i का मान √-1 है। यानी, $i^2$ = -1.

यदि k एक पूर्णांक है, तो:
$i^{4k + 1} = i$
$i^{4k + 2} = i^2 = -1$
$i^{4k + 3} = i^3 = (-1)i = -i$
$i^{4k + 4} = i^4 = 1$

हम i के नकारात्मक घाताकों को भी ज्ञात कर सकते हैं।

उदाहरण के लिए, $i^{-1} = 1/i = (1/i) × (i/i) = i/i^2 = i/(-1) = -i$

सम्मिश्र संख्याओं का निरपेक्ष मान (Absolute Value of Complex Numbers)

किसी वास्तविक संख्या का निरपेक्ष मान उस संख्या का धनात्मक मान होता है। इसे मापांक (modulus) द्वारा निरूपित किया जाता है।

उदाहरण के लिए, 5 का निरपेक्ष मान, अर्थात |5| = 5
-5 का निरपेक्ष मान, अर्थात |-5| = 5

सम्मिश्र संख्याओं के मामले में, हम निरपेक्ष मान की गणना कुछ अलग तरीके से करते हैं। यदि z = a + ib एक सम्मिश्र संख्या है, तो:

z का निरपेक्ष मान = |z| = |a + ib| = $√(a^2 + b^2)$

उदाहरण के लिए, 3 + 4i का निरपेक्ष मान = |3 + 4i| = $√(3^2 + 4^2) = √(9 + 16) = √25$ = 5

यदि $z_1$ और $z_2$ दो सम्मिश्र संख्याएँ हैं, तो:
$|z_1 + z_2| ≤ |z_1|+|z_2|$

आइए कुछ उदाहरण देखें।

अगर $z_1$ = 3 + 4i, और $z_2$ = 6 + 8i, तो:
$z_1 + z_2$ = (3 + 4i) + (6 + 8i) = 9 + 12i
$|z_1| = √(3^2 + 4^2)$ = 5
$|z_2| = √(6^2 + 8^2)$ = 10
$|z_1 + z_2| = √(9^2 + 12^2) = √225$ = 15
अब, 15 = 5 + 10

अगर $z_1$ = 1 - 2i, और $z_2$ = 3 + 5i, तो:
$z_1 + z_2$ = (1 - 2i) + (3 + 5i) = 4 + 3i
$|z_1| = √(1^2 + 2^2) = √5$
$|z_2| = √(3^2 + 5^2) = √34$
$|z_1 + z_2| = √(4^2 + 3^2)$ = 5
अब, 5 < √5 + √34

सम्मिश्र संख्याओं का संयुग्म (Conjugate of Complex Numbers)

यदि हमारे पास एक सम्मिश्र संख्या z = a + ib है, तो इसका संयुग्म z̄ = a – ib होगा। एक सम्मिश्र संख्या z के संयुग्म को सम्मिश्र संख्या, अर्थात z̄ के ऊपर एक दंड द्वारा निरूपित किया जाता है।

दो संयुग्मित सम्मिश्र संख्याओं के योग और गुणा से एक वास्तविक संख्या प्राप्त होती है। दूसरे शब्दों में, यदि दो सम्मिश्र संख्याओं का योग और गुणनफल वास्तविक है, तो उन दो सम्मिश्र संख्याओं को एक दूसरे से संयुग्मित होना चाहिए।

नोट

आप सम्मिश्र संख्याओं के लिए निम्नलिखित ग्राफ-निर्माता सॉफ्टवेयर का उपयोग कर सकते हैं। यह किसी सम्मिश्र संख्या के संयुग्म को भी दर्शाता है।

सम्मिश्र संख्याएं और उनके संयुग्म (Complex numbers & their Conjugates)

सम्मिश्र संख्याओं पर बीजगणितीय संक्रियाएँ (Algebraic Operations on Complex Numbers)

वास्तविक संख्याओं की तरह, हम सम्मिश्र संख्याओं पर भी जोड़, घटाव, गुणा और भाग की संक्रियाएँ कर सकते हैं।

सम्मिश्र संख्याओं का जोड़ और घटाव

सम्मिश्र संख्याओं को जोड़ते या घटाते समय, हम वास्तविक भागों और काल्पनिक भागों को अलग-अलग जोड़ते / घटाते हैं।

(a + ib) + (x +iy) = (a + x) + i(b + y)
(a + ib) - (x +iy) = (a - x) + i(b - y)

नोट

सम्मिश्र संख्याएँ योग के क्रमविनिमेय नियम (commutative law of addition) का पालन करती हैं, अर्थात् $z_1 + z_2 = z_2 + z_1$
सम्मिश्र संख्याएँ योग के साहचर्य नियम (associative law of addition) का भी पालन करती हैं, अर्थात् $(z_1 + z_2) + z_3 = z_1 + (z_2 + z_3)$

सम्मिश्र संख्याओं का गुणन

सम्मिश्र संख्याओं के गुणन में, हम दो द्विपदों (binomials) को गुणा करने की प्रक्रिया के समान प्रक्रिया का पालन करते हैं, अर्थात वितरण गुणन (distributive multiplication)।

$(a + ib) . (x + iy) = ax + i^2 by + iay + ibx = (ax - by) + i(ay + bx)$
(क्यूंकि $i^2$ = -1)

चेतावनी

जहाँ तक काल्पनिक संख्याओं के गुणन का संबंध है, निम्नलिखित बातों का ध्यान रखें। काल्पनिक संख्याओं के मामले में √p × √q, pq के बराबर नहीं होता है।

उदाहरण के लिए, i × i = √-1 × √-1 = √(-1 × -1) = √1 = 1 (गलत)
हम जानते हैं कि, $i^2$ = -1 (1 नहीं)

नोट

सम्मिश्र संख्याएँ गुणन के क्रमविनिमेय नियम (commutative law of multiplication) का पालन करती हैं, अर्थात् $z_1 . z_2 = z_2 . z_1$
सम्मिश्र संख्याएँ गुणन के साहचर्य नियम (associative law of multiplication) का भी पालन करती हैं, अर्थात् $(z_1 . z_2) . z_3 = z_1 . (z_2 . z_3)$
सम्मिश्र संख्याएँ वितरण नियम (distributive law) का भी पालन करती हैं, अर्थात् $z_1 . (z_2 + z_3) = z_1 . z_2 + z_1 . z_3$

सम्मिश्र संख्याओं का विभाजन

दो सम्मिश्र संख्याओं का विभाजन करते समय, हम हर में स्तिथ सम्मिश्र संख्या के संयुग्म (conjugate of the complex number in the denominator) के साथ अंश और हर दोनों को गुणा करते हैं। फिर हम इसे सरल करते हैं।

$\frac{a + ib}{x + iy} = \frac{(a + ib) . (x - iy)}{(x + iy) . (x - iy)} = \frac{ax + by + i(bx - ay)}{x^2 + y^2} = \frac{(ax + by)}{(x^2 + y^2)} + i \frac{(bx - ay)}{(x^2 + y^2)}$

नोट

सम्मिश्र संख्याओं के लिए आप निम्नलिखित ग्राफ कैलकुलेटर का उपयोग कर सकते हैं।

Complex number elementary operations

सम्मिश्र संख्या सर्वसमिकाएँ (Complex Number Identities)

वर्ग (Squares)

$(z_1 + z_2)^2 = (z_1)^2 + (z_2)^2 + 2 z_1 × z_2$
$(z_1 – z_2)^2 = (z_1)^2 + (z_2)^2 – 2 z_1 × z_2$
$(z_1)^2 – (z_2)^2 = (z_1 + z_2)(z_1 – z_2)$

घन (Cubes)

$(z_1 + z_2)^3 = (z_1)^3 + 3(z_1)^2 z_2 + 3(z_2)^2 z_1 + (z_2)^3$
$(z_1 – z_2)^3 = (z_1)^3 – 3(z_1)^2 z_2 + 3(z_2)^2 z_1 – (z_2)^3$