डिफरेंशियल कैलकुलस की मूल अवधारणाएं (Basics of Differential Calculus)

Jan 15, 2022 calculus
Share on:
डिफरेंशियल कैलकुलस की मूल अवधारणाएं (Basics of Differential Calculus)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Basics of Differential Calculus, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

इस लेख में, हम डिफरेंशियल कैलकुलस (या अवकलन, या Differential Calculus) की मूल अवधारणाओं और नियमों के बारे में अध्ययन करेंगे। लेकिन ऐसा करने से पहले, आइए समझते हैं कि आखिर कैलकुलस (या कलन, या Calculus) क्या होता है।

कैलकुलस (या कलन, या Calculus) एक लैटिन शब्द है जिसका अर्थ है "कंकड़"। यह गणित की एक शाखा है, जो किसी बड़ी घटना को उसके छोटे-छोटे हिस्सों को देखकर समझने की कोशिश करती है।

यहां हम मूल रूप से बहुत छोटे अंतरों के योग (summation of infinitesimal differences) पर आधारित विधियों द्वारा, फलनों (functions) के डेरिवेटिव (derivatives) और इंटीग्रल (integrals) ज्ञात करते हैं।

कैलकुलस की दो मुख्य शाखाएँ होती हैं:

डिफरेंशियल कैलकुलस / Differential Calculus (डेरिवेटिव, Derivatives) - इसका उपयोग किसी चीज को छोटे टुकड़ों में काटने के लिए किया जाता है, ताकि यह पता लगाया जा सके कि यह कैसे बदलती है। किसी फलन का डेरिवेटिव, उस फलन की "परिवर्तन की दर" है, जिसे उस फलन की ढलान (slope) के द्वारा दर्शाया जाता है।

इंटीग्रल कैलकुलस / Integral Calculus (इंटीग्रल, Integration) - इसका उपयोग छोटे टुकड़ों को एक साथ जोड़ने (यानी एकीकृत) करने के लिए किया जाता है, ताकि कुल मात्रा का पता लगाया जा सके, जैसे कि क्षेत्रफल, आयतन, केंद्रीय बिंदु, आदि।

नोट

डिफरेंशियल इक्वेशन (Differential Equation) एक समीकरण होती है, जिसमें एक फलन और उसके एक या अधिक डेरिवेटिव (derivatives) शामिल होते हैं।

कभी-कभी हम किसी दिए गए फलन के परिवर्तन की दर जानने में रुचि रखते हैं। यह एक वक्र पर दो बिंदुओं को मिलाने वाली रेखा का ढलान (slope) ज्ञात करके किया जा सकता है।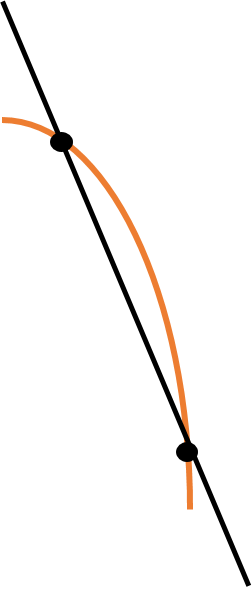
Calculus

Calculus

ढलान (Slope) = Yमेंपरिवर्तनXमेंपरिवर्तन=y1−y2x1−x2\frac{Y \hspace{1ex} में \hspace{1ex} परिवर्तन}{X \hspace{1ex} में \hspace{1ex} परिवर्तन} = \frac{y_1 - y_2}{x_1 - x_2}

दो बिंदु जितने करीब होंगे, हमें उतना ही सटीक परिणाम मिलेगा। यदि दो बिंदुओं के बीच की दूरी को अनंत रूप से कम (अर्थात लगभग शून्य) कर दिया जाता है, तो हम किसी एक निश्चित बिंदु पर फलन की परिवर्तन की तात्कालिक दर (instantaneous rate of change) पा सकते हैं।
Calculus

Calculus

फलन के डेरिवेटिव (अवकलज, derivative) को ढूंढकर हम यही करते हैं। अर्थात्, किसी फलन का डेरिवेटिव एक निश्चित बिंदु पर उस फलन की परिवर्तन की तात्कालिक दर (या ढलान) होता है।

फलनों के डेरिवेटिव खोजने के लिए, हम differentiation की विधि का उपयोग करते हैं। इसे डिफरेंशियल कैलकुलस (Differential Calculus) कहा जाता है।

नोट

किसी फलन f(x) का Derivative f'(x) या ddx\frac{d}{dx} द्वारा निरूपित किया जाता है|

तो, f(x) का Derivative f'(x) के बराबर होता है, या f(x) का d dx, f'(x) के बराबर होता है।

आइए, इस प्रक्रिया को गणितीय रूप से और कुछ उदाहरणों का उपयोग करके समझने का प्रयास करें।

यदि हमारे पास एक फलन, y = f(x) है, तो इनपुट को x से (x + x) में बदलने पर, आउटपुट f(x) या y से f(x + Δx) या (y + Δy) में बदल जाता है। .

ढलान (Slope) = Yमेंपरिवर्तनXमेंपरिवर्तन=ΔyΔx=f(x+Δx)−f(x)Δx\frac{Y \hspace{1ex} में \hspace{1ex} परिवर्तन}{X \hspace{1ex} में \hspace{1ex} परिवर्तन} = \frac{Δy}{Δx} = \frac{f(x + Δx) - f(x)}{Δx}

जैसे-जैसे Δx शून्य के करीब जाता है, हमें एक निश्चित बिंदु पर फलन की तात्कालिक परिवर्तन दर प्राप्त होगी। फलन के derivatives खोजने के दौरान हम यही करते हैं।

अर्थात्, एक फलन f(x) का derivative होगा:
f'(x) = lim⁡Δx→0f(x+Δx)−f(x)Δx\lim_{Δx\to 0} \frac{f(x + Δx) - f(x)}{Δx}

आइए, एक उदाहरण देखें।

प्रश्न. फलन f(x) = x2x^2 का अवकलज (derivative) ज्ञात कीजिए|

व्याख्या:

हम जानते हैं कि, f(x) = x2x^2

तो, f(x + Δx) = (x+Δx)2=x2+2xΔx+(Δx)2(x + Δx)^2 = x^2 + 2xΔx + (Δx)^2

अब, ढलान (Slope) = ΔyΔx=f(x+Δx)−f(x)Δx=x2+2xΔx+(Δx)2−x2Δx=2xΔx+(Δx)2Δx=2x+Δx\frac{Δy}{Δx} = \frac{f(x + Δx) - f(x)}{Δx} = \frac{x^2 + 2xΔx + (Δx)^2 - x^2}{Δx} = \frac{2xΔx + (Δx)^2}{Δx} = 2x + Δx

जैसे-जैसे, Δx 0 की ओर जाता है, (2x + Δx) का मान 2x की ओर बढ़ेगा। यानी, lim⁡Δx→0(2x+Δx)\lim_{Δx\to 0} (2x + Δx) = 2x

तो, फलन f(x) = x2x^2 का derivative, ddxx2\frac{d}{dx} x^2 = 2x.

दूसरे शब्दों में, किसी दिए गए बिंदु पर इस फलन का ढाल 2x होगा। चूंकि x एक चर (variable) है, वक्र का ढलान विभिन्न बिंदुओं पर भिन्न होगा।


नोट

अधिकांश वक्रों के ढलान में स्थिर और परिवर्तनशील दोनों घटक होते हैं, जैसे की 2x, 3x2x^2, आदि। इसलिए, वक्र का ढलान भिन्न-भिन्न होता है - यह इस बात पर निर्भर करता है कि हम इसे वक्र पर कहाँ माप रहे हैं।

इसके विपरीत, सभी सीधी रेखाओं का ढलान स्थिर होता है, जैसे की 2, 5, -3, आदि। इसलिए, एक सीधी रेखा का ढलान स्थिर रहता है, चाहे हम उसे रेखा पर कहीं भी माप रहे हों।

आइए देखें कैसे। हम सरल रेखा y = 3x का derivative (अवकलज) ज्ञात करेंगे।

हम जानते हैं कि, ढाल (Slope) = ΔyΔx=f(x+Δx)−f(x)Δx=3(x+Δx)−3xΔx=3ΔxΔx\frac{Δy}{Δx} = \frac{f(x + Δx) - f(x)}{Δx} = \frac{3(x + Δx) - 3x}{Δx} = \frac{3Δx}{Δx} = 3

तो, 3x का derivative 3 के बराबर है (अर्थात एक स्थिरांक है)

हालांकि, हमें परीक्षा में प्रत्येक फलन के derivative को निकालने का पर्याप्त समय नहीं मिलता है। इसलिए, हमें कुछ सबसे सामान्य फलनों (जैसे कि x2x^2, x3x^3, sin x, cos x, आदि) के derivatives को याद रखना चाहिए।

यहां कुछ सामान्य फलनों के Derivatives की सूची दी गई है जिनका हम सामना करेंगे। हालाँकि हम इनको ठीक उसी तरह निकाल सकते हैं, जैसे हमने ऊपर कुछ फलनों के मामले में किया था। परन्तु, परीक्षा में हमारी गति को तेज करने के लिए इनको याद कर लेना एक अच्छा विचार होगा।

किसी स्थिरांक का Derivative हमेशा शून्य होता है।

ddxc\frac{d}{dx} c = 0


(जहाँ c एक स्थिरांक है)

किसी सीधी रेखा का derivative हमेशा एक अचल (स्थिरांक, constant) होता है।

ddxx\frac{d}{dx} x = 1

ddxcx\frac{d}{dx} cx = c


(जहाँ c एक स्थिरांक है)

ddxxn=nxn−1\frac{d}{dx} x^n = n x^{n - 1}

तो, आइए उपरोक्त नियम के आधार पर कुछ फलनों के derivatives देखें।

ddxx2\frac{d}{dx} x^2 = 2x

ddxx3=3x2\frac{d}{dx} x^3 = 3 x^2

ddxx1/2=(1/2)x−1/2\frac{d}{dx} x^{1/2} = (1/2) x^{-1/2}

ddxx−1=−x−2\frac{d}{dx} x^{-1} = -x^{-2}

ddxx−2=−2x−3\frac{d}{dx} x^{-2} = -2x^{-3}

ddxex=ex\frac{d}{dx} e^x = e^x

ddxax=ln(a)ax\frac{d}{dx} a^x = ln(a) \hspace{1ex} a^x

ddxln(x)=1x\frac{d}{dx} ln(x) = \frac{1}{x}

ddxloga(x)=1xln(a)\frac{d}{dx} log_a(x) = \frac{1}{x \hspace{1ex} ln(a)}

ddxsinx=cosx\frac{d}{dx} sin x = cos x

ddxcosx=−sinx\frac{d}{dx} cos x = - sin x

ddxtanx=sec2x\frac{d}{dx} tan x = sec^2 x

ddxsin−1x=11−x2\frac{d}{dx} sin^{-1} x = \frac{1}{\sqrt{1 - x^2}}

ddxcos−1x=−11−x2\frac{d}{dx} cos^{-1} x = - \frac{1}{\sqrt{1 - x^2}}

ddxtan−1x=11+x2\frac{d}{dx} tan^{-1} x = \frac{1}{1 + x^2}

नोट

x रेडियन (radians) में होना चाहिए।

comments powered by Disqus