कैलेंडर की मूल अवधारणाएं (Basics of Calendar)

Overview

इस लेख में हम रीजनिंग के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Basics of Calendar, in Hindi

नोट

कैलेंडर से सम्बंधित और लेख आप यहाँ पढ़ सकते हैं :

• किसी तारीख पर पड़ने वाला दिन ज्ञात करना
• कैलेंडर कैसे दोहराते हैं ?

कैलेंडर दिन, सप्ताह और महीने की एक व्यवस्था है।

ग्रेगोरियन कैलेंडर (Gregorian calendar) दुनिया का सबसे लोकप्रिय कैलेंडर है। यह भारतीय राष्ट्रीय कैलेंडर भी है।

माना जाता है कि हर दिन की शुरुआत आधी रात से होती है।

नोट

1 जनवरी 0001 सोमवार था।

• दिन
  हर 24 घंटे में एक दिन बनता है। यह कैलेंडर की सबसे छोटी इकाई है।
  एक दिन सप्ताह का सातवाँ भाग होता है।

• सप्ताह
  यह 7 दिनों का समूह है: रविवार, सोमवार, मंगलवार, बुधवार, गुरुवार, शुक्रवार, शनिवार

नोट

कल = आज – 1 दिन

कल = आज + 1 दिन

कल से पहले का दिन = आज – 2 दिन

परसों = आज + 2 दिन

प्र. यदि आज रविवार है, तो कल के 3 दिन बाद सप्ताह का कौन सा दिन होगा?

(a) गुरुवार (b) बुधवार (c) शनिवार (d) शुक्रवार 

व्याख्या:

प्र. यदि परसों से पहले का दिन बुधवार था, तो रविवार कब होगा?

(a) आज के 3 दिन बाद (b) कल (c) आज (d) परसों

व्याख्या:

• माह
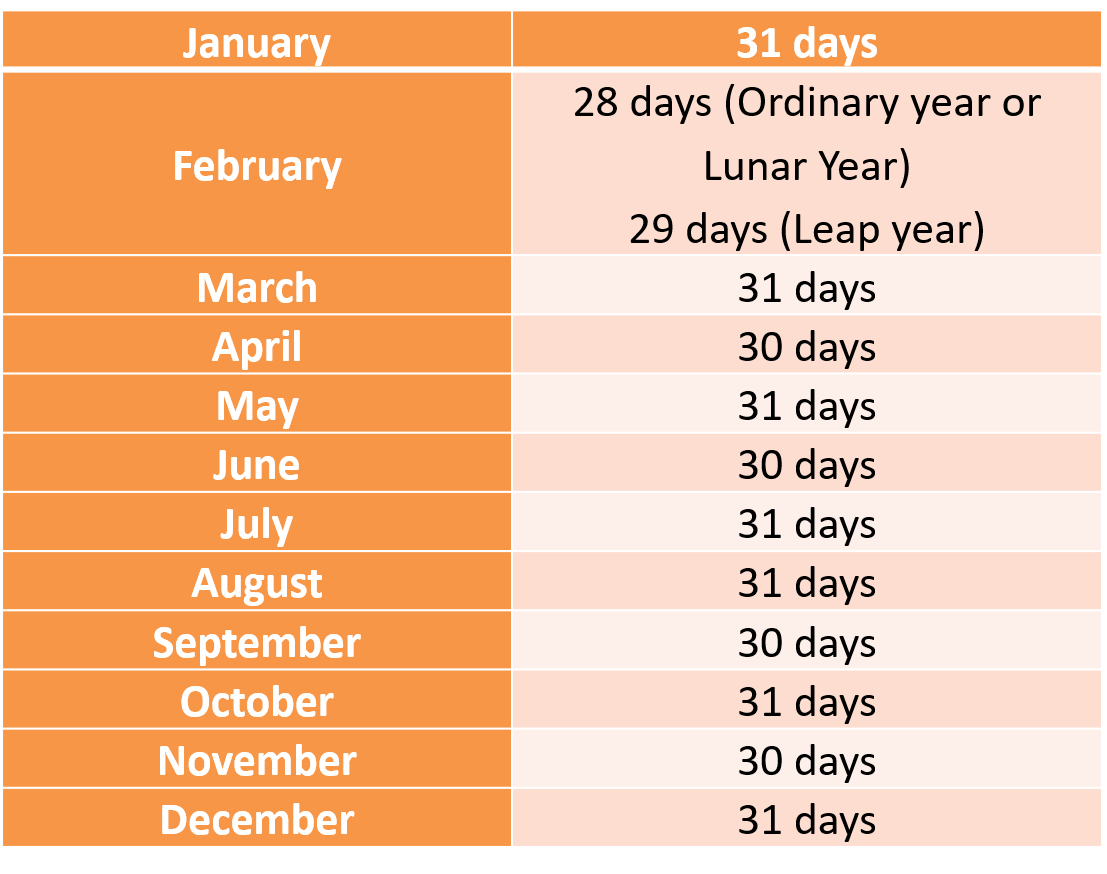
  एक महीना साल का 12वां हिस्सा होता है। इसमें 28, 29, 30 या 31 दिन होते हैं।
  साल में 12 महीने होते हैं।
  

  calendar

• वर्ष
  यह पृथ्वी द्वारा सूर्य के चारों ओर एक चक्कर लगाने में लगने वाला समय है। एक साल में 12 महीने होते हैं। एक साल एक सदी का 100वां हिस्सा होता है।

• सदी
  100 साल के ब्लॉक को सदी कहा जाता है।
  सदी के वर्षों के उदाहरण: 1100, 1800, 2000, 2100, 2900 आदि।

विभिन्न प्रकार के प्रश्न

• कैलेंडर दोहराव
• किसी विशेष तिथि पर दिन ढूँढना (आमतौर पर, इस प्रयोजन हेतु एक संदर्भ दिन दिया जाता है)

साधारण और अधिवर्ष की अवधारणा (Concept of Ordinary and Leap years)

साधारण वर्ष (Ordinary Year)

एक साधारण वर्ष एक ऐसा वर्ष होता है जिसमें 365 दिन (52 सप्ताह + 1 विषम दिन) होते हैं।

ऐसे वर्ष 4 से विभाज्य नहीं होते हैं, जैसे की 2001, 2002, 2003, 2005, 2006, 2007, 2009, 2010 और 2011, आदि।

अगर शताब्दी वर्षों की बात की जाये, तो शताब्दी साधारण वर्ष 400 से पूर्णतः विभाज्य नहीं होते हैं, जैसे की 100, 200, 500, 600, 700 और 900 आदि।

साधारण वर्ष के गुण (Properties of Ordinary Year)

• एक सामान्य वर्ष में, वर्ष के पहले और अंतिम दिन समान होते हैं जैसे, एक सामान्य वर्ष में, यदि 1 जनवरी को सोमवार पड़ता है, तो 31 दिसंबर को भी सोमवार ही होगा।

• किन्हीं दो क्रमागत साधारण वर्षों में, अगले वर्ष की तिथि पिछले वर्ष की उसी तिथि से एक दिन आगे होगी| उदाहरण के लिए, यदि 2 अगस्त 2010 को मंगलवार है, तो 2 अगस्त 2011 को बुधवार होगा।

अधिवर्ष (Leap Year)

अधिवर्ष वह वर्ष होता है जिसमें 366 दिन (52 सप्ताह + 2 दिन) होते हैं।

ऐसे वर्ष 4 से पूर्णतः विभाज्य होते हैं, जैसे की 2004, 2008, 2012, 2016, आदि।

अगर शताब्दी वर्षों की बात की जाये, तो शताब्दी अधिवर्ष 400 से पूर्णतः विभाज्य होते हैं, जैसे की 400, 800, 1200, 1600, 2000, 2400 आदि।

नोट

अर्थार्थ, अधिवर्ष एक ऐसा वर्ष है जो 4 या 400 से विभाज्य होता है, लेकिन 100 से विभाज्य नहीं होता है।

अधिवर्ष के गुण (Properties of Leap Year)

• अधिवर्ष का अंतिम दिन पहले दिन से एक दिन आगे होता है| उदाहरण के लिए, अगर किसी अधिवर्ष में, 1 जनवरी, 2004 को सोमवार पड़ता है, तो 31 दिसंबर, 2004 को मंगलवार होगा।

नोट

निम्नलिखित लगातार पड़ रहे वर्षों पर विचार करें, और पैटर्न को देखें:
1 जनवरी 2015 - गुरुवार
1 जनवरी 2016 - शुक्रवार (2016 एक अधिवर्ष है)
1 जनवरी 2017 - रविवार
1 जनवरी 2018 - सोमवार
1 जनवरी 2019 - मंगलवार
1 जनवरी 2020 - बुधवार (2020 एक अधिवर्ष है)

प्रश्न. निम्नलिखित में से किस वर्ष के फरवरी माह में 29 दिन नहीं थे ?

(a) 2000     (b) 2004    (c) 1996    (d) 1966 

व्याख्या:

प्र. यदि शुक्रवार गैर-लीप वर्ष का पहला दिन है, तो वर्ष का अंतिम दिन कौन सा दिन होगा?

(a) शुक्रवार (b) रविवार (c) सोमवार (d) मंगलवार 

व्याख्या:

प्र. राम का जन्म 29 फरवरी को हुआ था। उन्होंने ठीक 29 फरवरी 2008 को चौथी बार अपना जन्मदिन मनाया। ज्ञात कीजिये की उनका जन्म किस वर्ष में हुआ था?

(a) 1992     (b) 2004    (c) 2000    (d) 1996 

व्याख्या:

विषम दिनों की अवधारणा (Concept of Odd days)

विषम दिनों की अवधारणा सप्ताह की अवधारणा से निकलती है।
सप्ताह की अवधारणा - हर सातवें दिन के बाद दिन दोहराया जाता है।

जैसे की - यदि आज सोमवार है, तो अब से 28वां दिन भी सोमवार होगा क्योंकि यह 7 (28/7 = 4, इसलिए चार सप्ताह) का गुणज है।

जैसे की - यदि आज सोमवार है, तो 30वां दिन = 28 + 2 (4 सप्ताह और 2 दिन), यानी 30/7 शेष 2 देगा।
ये दो दिन विषम दिन हैं। तो, दो विषम दिनों के साथ, 30 वां दिन बुधवार होगा।

नोट

अत: दी गई अवधि में विषम दिनों की संख्या = शेष {अवधि/7}
यानी, जो शेष बचेगा, वह विषम दिनों की संख्या होगी।

एक निश्चित अवधि में पूरे सप्ताह के अलावा अतिरिक्त दिन विषम दिन कहलाते हैं, जैसे:
7 दिनों की अवधि = 7 + 0 अतिरिक्त दिन = 0 विषम दिन
8 दिनों की अवधि = 7 + 1 अतिरिक्त दिन = 1 विषम दिन
9 दिनों की अवधि = 7 + 2 अतिरिक्त दिन = 2 विषम दिन
10 दिनों की अवधि = 7 + 3 अतिरिक्त दिन = 3 विषम दिन
11 दिनों की अवधि = 7 + 4 अतिरिक्त दिन = 4 विषम दिन
12 दिनों की अवधि = 7 + 5 अतिरिक्त दिन = 5 विषम दिन
13 दिनों की अवधि = 7 + 6 अतिरिक्त दिन = 6 विषम दिन
लेकिन 14 दिनों की अवधि = 7 + 7 = 2 पूर्ण सप्ताह = 0 विषम दिन

महीने में विषम दिन (Odd days in a Month)

विभिन्न महीनों में विषम दिनों की संख्या (Number of odd days in different months)

आरेख: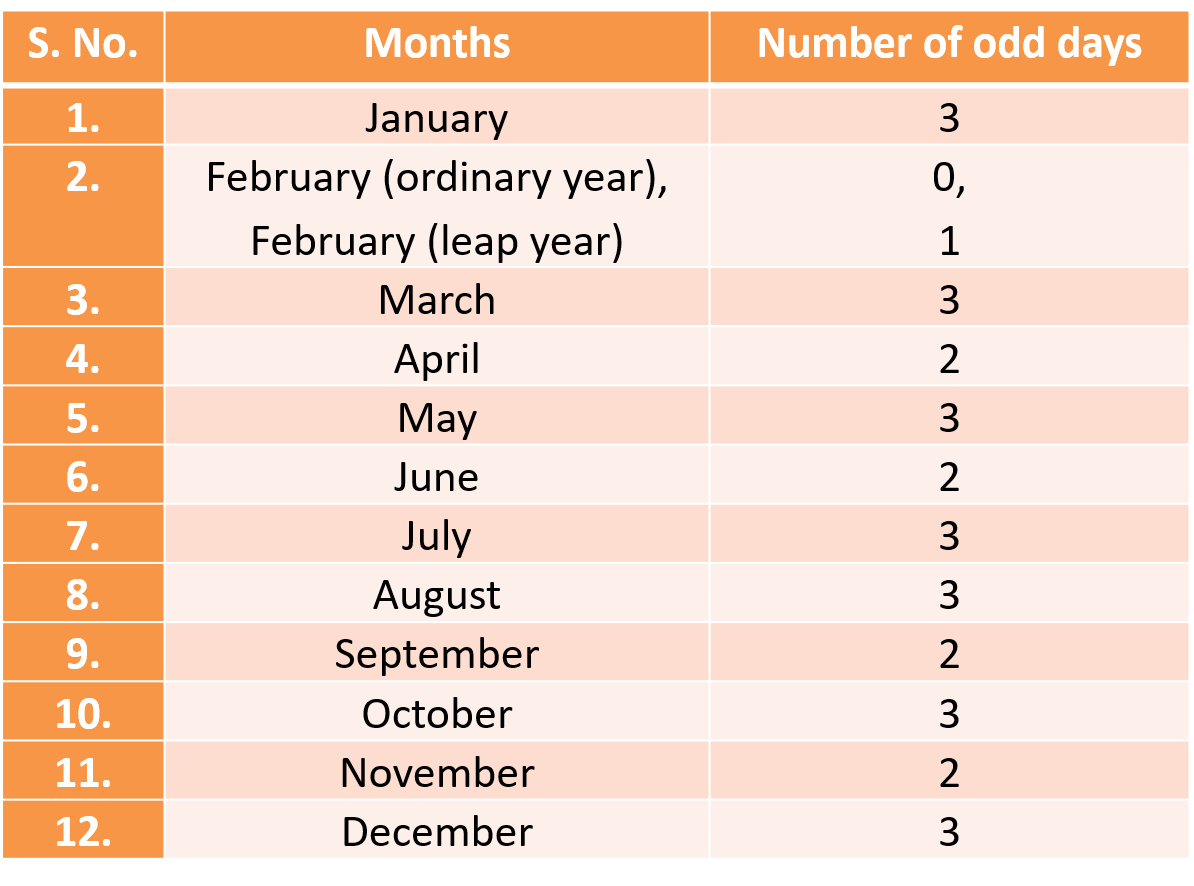

calendar

विभिन्न तिमाहियों में विषम दिनों की संख्या

जनवरी + फरवरी + मार्च = 6 या 7 (यानी 0)
अप्रैल + मई + जून = 7 (यानी 0)
जुलाई + अगस्त + सितंबर = 8 (यानी 1)
अक्टूबर + नवंबर + दिसंबर = 8 (यानी 1)

प्र. आज मंगलवार है, तो 72 दिन बाद कौन सा दिन होगा?

(a) रविवार (b) शुक्रवार (c) गुरुवार (d) शनिवार 

व्याख्या:

साल में विषम दिन (Odd days in a Year)

एक सामान्य वर्ष में विषम दिनों की संख्या

एक साधारण वर्ष में दिनों की संख्या = 365 = 364 + 1
एक साधारण वर्ष में विषम दिनों की संख्या = शेष {365/7} = 1 विषम दिन

एक लीप वर्ष में विषम दिनों की संख्या

एक लीप वर्ष में दिनों की संख्या = 366 = 364 + 2
एक लीप वर्ष में विषम दिनों की संख्या = शेष {366/7} = 2 विषम दिन

किन्ही 100 वर्षों में विषम दिनों की संख्या

100 वर्षों में विषम दिनों की संख्या = 76 साधारण वर्ष + 24 लीप वर्ष
= 76 साधारण वर्षों के 76 विषम दिन + (24 × 2) 24 लीप वर्ष के विषम दिन
= 76 विषम दिन + 48 विषम दिन = 124 विषम दिन
= (7 × 17 + 5) विषम दिन = 5 विषम दिन

चेतावनी

ऐसा तब होगा जब 100 वर्षों की गणना में 400 से विभाज्य शताब्दी वर्ष (जैसे 1600, 2000) न हो, वार्ना हमें 1 और विषम दिन जोड़ना होगा।

प्र. यदि 1 जनवरी 1901 को मंगलवार था, तो 1 जनवरी 2001 को कौन सा दिन था?

(a) रविवार (b) मंगलवार (c) सोमवार (d) शनिवार 

व्याख्या:

200 वर्षों में विषम दिनों की संख्या

200 वर्ष में विषम दिन = (100 वर्ष में विषम दिन) × 2 = 5 × 2 = 10 दिन = 1 सप्ताह + 3 दिन = 3 विषम दिन

चेतावनी

ऐसा तब होगा जब 400 से विभाज्य शताब्दी वर्ष (जैसे 1600, 2000) 200 वर्षों में नहीं गिना जाता है, वार्ना फिर 1 और विषम दिन जोड़ना होगा।

300 वर्षों में विषम दिनों की संख्या

300 वर्षों में विषम दिन = (100 वर्षों में विषम दिन) × 3 = 5 × 3 = 15 दिन = 2 सप्ताह + 1 दिन = 1 विषम दिन

चेतावनी

ऐसा तब होगा जब 300 से विभाज्य शताब्दी वर्ष (जैसे 1600, 2000) 200 वर्षों में नहीं गिना जाता है, वार्ना फिर 1 और विषम दिन जोड़ना होगा।

400 वर्षों में विषम दिनों की संख्या

400 वर्षों में विषम दिन = (100 वर्ष में विषम दिन) × 4 + 1 दिन = (5 × 4 + 1) दिन = 21 दिन = 3 सप्ताह = 0 विषम दिन

नोट

यदि हम किसी भी क्रमागत 400 वर्षों की गणना करते हैं, तो 400 से विभाज्य शताब्दी वर्ष (जैसे 1600, 2000) हमेशा गिना ही जाएगा।

विभिन्न वर्षों की समान तारीख के दिन जानना (Finding day on the same date)

अगर आज सोमवार है, तो क्या आप बता सकते हैं कि अगले साल या पिछले साल उसी तारीख को कौन सा दिन होगा , या था ?

यह आसान है। बस इसे याद रखें:

• यदि 29 फरवरी लगातार वर्षों की दो दी गई तिथियों के बीच में आती है, तो दोनों तिथियों के बीच 2 विषम दिन होंगे।
• यदि दो क्रमागत वर्षों की दी गई तिथियों के बीच 29 फरवरी नहीं है, तो उनके बीच केवल 1 विषम दिन होगा।

आइए कुछ उदाहरण देखें:

प्र. 6 मार्च 1992 को गुरुवार था| 6 मार्च 1993 को सप्ताह का कौन सा दिन होगा?

(a) शुक्रवार (b) गुरुवार (c) सोमवार (d) शनिवार 

व्याख्या:

प्र. 6 जनवरी 1992 को गुरुवार था| 6 जनवरी 1993 को सप्ताह का कौन सा दिन होगा?

(a) शुक्रवार (b) गुरुवार (c) सोमवार (d) शनिवार 

व्याख्या: