क्षेत्रमिति - गोला (Mensuration - Sphere)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Sphere, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• क्षेत्रमिति क्या होती है?
• क्षेत्रमिति - घन और घनाभ
• क्षेत्रमिति - गोला
• क्षेत्रमिति - बेलन
• क्षेत्रमिति - शंकु
• क्षेत्रमिति - प्रिज्म
• क्षेत्रमिति - पिरामिड

इस लेख में, हम क्षेत्रमिति के एक महत्वपूर्ण विषय, गोले से संबंधित अवधारणाओं और सूत्रों के बारे में जानने जा रहे हैं।

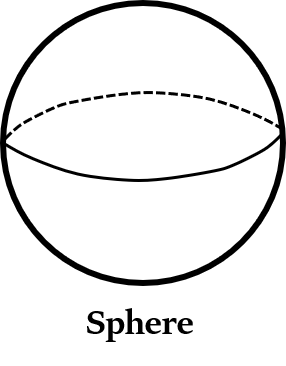
गोला क्या होता है? (What is a Sphere?)

गोला (Sphere) एक त्रि-आयामी ठोस गोल संरचना है, इस प्रकार कि इसकी सतह पर स्तिथ प्रत्येक बिंदु इसके केंद्र से समान दूरी पर होता है।

Mensuration

गोलार्द्ध (Hemisphere) एक गोले का आधा भाग होता है।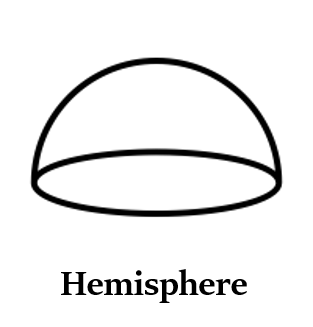

Mensuration

गोले और गोलार्ध से संबंधित सूत्र (Formulae related to Sphere and Hemisphere)

यदि 'r' त्रिज्या (radius) है, और 'd' गोले/गोलार्ध का व्यास (diameter) है, तो:

सूत्र 1: आयतन (Volume)

गोले का आयतन = $\frac{4}{3} πr^3 = \frac{1}{6} πd^3$

खोखले गोले का आयतन = पूरे गोले का आयतन - भीतरी खाली जगह का आयतन = $\frac{4}{3} πR^3 - \frac{4}{3} πr^3 = \frac{4}{3} π (R^3 – r^3) = \frac{1}{6} π (D^3 – d^3)$

गोलार्द्ध का आयतन = $\frac{2}{3} πr^3 = \frac{1}{6} πd^3$

सूत्र 2: पृष्ठीय क्षेत्रफल (Surface Area)

गोले का पृष्ठीय क्षेत्रफल (Surface area) = 4π $r^2 = π d^2$

गोलार्द्ध का वक्र पृष्ठीय क्षेत्रफल (Curved Surface area) = 2π $r^2$

गोलार्द्ध का कुल पृष्ठीय क्षेत्रफल (Total Surface area) = 2π $r^2 + πr^2 = 3πr^2$