विभाज्यता की अवधारणा (Concept of Divisibility)

Overview

इस लेख में हम क्वांटिटेटिव एप्टीटुड (गणित) के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Concept of Divisibility, in Hindi

नोट

इस अध्याय से सम्बंधित, अन्य विषयों के बारे में जानने के लिए आप हमारे निम्नलिखित लेख पढ़ सकते हैं:

• गणित में संख्याओं के प्रकार
• क्रमागत संख्याएं क्या होती हैं?
• भिन्न क्या होता है?
• को-प्राइम क्या होते हैं?
• क्रमगुणित की अवधारणा
• गुणनखंड और गुणज क्या होते हैं?
• चक्रीयता विधि क्या होती है?
• शेष प्रमेय
• कई संख्याओं के शेष
• विभाज्यता की अवधारणा
• LCM और HCF की अवधारणा

इस लेख में, हम विभाज्यता की अवधारणा (Concept of Divisibility) के बारे में अध्ययन करेंगे।

A और B दो पूर्णांक (integers, सकारात्मक या नकारात्मक) हैं, जहाँ B ≠ 0

यदि A/B एक पूर्णांक है, तो हम कह सकते हैं कि A, B से विभाज्य है (या A, B का गुणज, multiple है)।

जैस की, यदि A = 18 और B = 3, तो 18/3 = 6. अतः, 18, 3 से विभाज्य है।

नोट

8, 4 और -4 दोनों से विभाज्य है।
हालांकि, ध्यान दें कि 8, 4 का गुणज है लेकिन -4 का गुणज नहीं है।

नोट

0 (शून्य), 0 (शून्य) को छोड़कर सभी पूर्णांकों से विभाज्य (divisible) होता है।

विभाज्यता नियम (Divisibility Rule)

विभाज्यता नियम (Divisibility rule) – यह पता लगाने के लिए कि क्या कोई संख्या किसी अन्य संख्या से विभाज्य है (वास्तव में विभाजन किए बिना )। यह उनके अंकों (digits) की जांच करके किया जाता है।

एक संख्या दूसरी संख्या से विभाज्य है या नहीं, यह पता लगाने के लिए हमें दो बुनियादी बातों का ध्यान रखना चाहिए:

• यदि भाजक एक अभाज्य संख्या (prime number) है: हमें केवल उस संख्या के लिए विभाज्यता नियम लागू करने की आवश्यकता है।
  
  उदा. क्या 215, 5 से विभाज्य है?
  5 एक अभाज्य संख्या है। इसलिए, हमें केवल 5 के लिए विभाज्यता नियम लागू करने की आवश्यकता है।

• यदि भाजक एक भाज्य संख्या (समग्र, composite number) है: हमें भाजक के सह-अभाज्य गुणनखंड (co-prime factors) खोजने होंगे और फिर ऐसे प्रत्येक गुणनखंड के लिए विभाज्यता नियम लागू करना होगा। संख्या भाजक से विभाज्य होगी, यदि यह इन सभी सह-अभाज्य गुणनखंडों से विभाज्य है।
  
  उदा. क्या 156, 12 से विभाज्य है?
  12 = 4 × 3
  4 और 3 सह-अभाज्य संख्याएँ हैं। इसलिए, हमें सिर्फ 4 और 3 के लिए विभाज्यता नियम लागू करने की आवश्यकता है।

5, 10 के लिए विभाज्यता नियम (Divisibility Rule for 5, 10)

कोई संख्या 5 से विभाज्य होती है, यदि उसकी इकाई का अंक या तो 0 या 5 है।

उदा. 310 और 465, 5 से विभाज्य हैं।
311 और 464, 5 से विभाज्य नहीं हैं।

कोई संख्या 10 से विभाज्य होती है, यदि उसकी इकाई का अंक 0 है।

उदा. 310 और 460, 10 से विभाज्य हैं।
611 और 564, 10 से विभाज्य नहीं हैं।

2, 4, 8, 16 के लिए विभाज्यता नियम (Divisibility Rule for 2, 4, 8, 16)

एक संख्या 2 से विभाज्य होती है, यदि उसकी इकाई का अंक 0, 2, 4, 6 या 8 है, अर्थात यदि इकाई का अंक 2 से विभाज्य है।

उदा. 124, 2 से विभाज्य है, क्योंकि 4, 2 से विभाज्य है।
613, 2 से विभाज्य नहीं है, क्योंकि 3, 2 से विभाज्य नहीं है।

एक संख्या 4 से विभाज्य होती है, यदि उसके अंतिम दो अंकों से बनी संख्या 4 से विभाज्य हो।

उदा. 124, 4 से विभाज्य है, क्योंकि 24, 4 से विभाज्य है।
613, 4 से विभाज्य नहीं है, क्योंकि 13, 4 से विभाज्य नहीं है।

एक संख्या 8 से विभाज्य होती है, यदि उसके अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य हो।

उदा. 124, 8 से विभाज्य है, क्योंकि 24, 8 से विभाज्य है।
613, 8 से विभाज्य नहीं है, क्योंकि 13, 8 से विभाज्य नहीं है।

कोई संख्या 16 से विभाज्य होती है, यदि उसके अंतिम चार अंकों से बनी संख्या 16 से विभाज्य हो।

उदा. 5112, 16 से विभाज्य है, क्योंकि 112, 16 से विभाज्य है।
6415, 16 से विभाज्य नहीं है, क्योंकि 415, 16 से विभाज्य नहीं है।

3, 9 के लिए विभाज्यता नियम (Divisibility Rule for 3, 9)

एक संख्या 3 से विभाज्य होती है, यदि उसके अंकों का योग 3 से विभाज्य हो।

उदा. 123, 3 से विभाज्य है, क्योंकि (1 + 2 + 3 = 6), 3 से विभाज्य है।
1363, 3 से विभाज्य नहीं है, क्योंकि (1 + 3 + 6 + 3 = 13), 3 से विभाज्य नहीं है।

एक संख्या 9 से विभाज्य होती है, यदि उसके अंकों का योग 9 से विभाज्य हो।

उदा. 126, 9 से विभाज्य है, क्योंकि (1 + 2 + 6 = 9), 9 से विभाज्य है।
123, 9 से विभाज्य नहीं है, क्योंकि (1 + 2 + 3 = 6), 9 से विभाज्य नहीं है।

6, 12, 14, 15, 18, 21, आदि से विभाज्यता (Divisibility by 6, 12, 14, 15, 18, 21, etc.)

इन भाज्य संख्याओं (composite numbers) के लिए, हम सह-अभाज्य गुणनखंड विधि (Co-prime factor method) का उपयोग करेंगे।

यह जांचने के लिए कि दी गई संख्या 6, 12, 14, 15, 18, 21 आदि से विभाज्य है या नहीं, हमें यह जांचना होगा कि दी गई संख्या इन भाजक के सह-अभाज्य गुणनखंडों (co-prime factors) से विभाज्य है या नहीं।

यदि कोई संख्या x और y (जहाँ x और y सह-अभाज्य हैं) से विभाज्य है, तो दी गई संख्या xy से विभाज्य होगी।

उदाहरण: 6 = 2 x 3. अतः, कोई भी संख्या जो 2 और 3 से विभाज्य है, वह 6 से भी विभाज्य होगी।
186, 2 और 3 दोनों से विभाज्य है, इसलिए 186, 6 से भी विभाज्य होगी।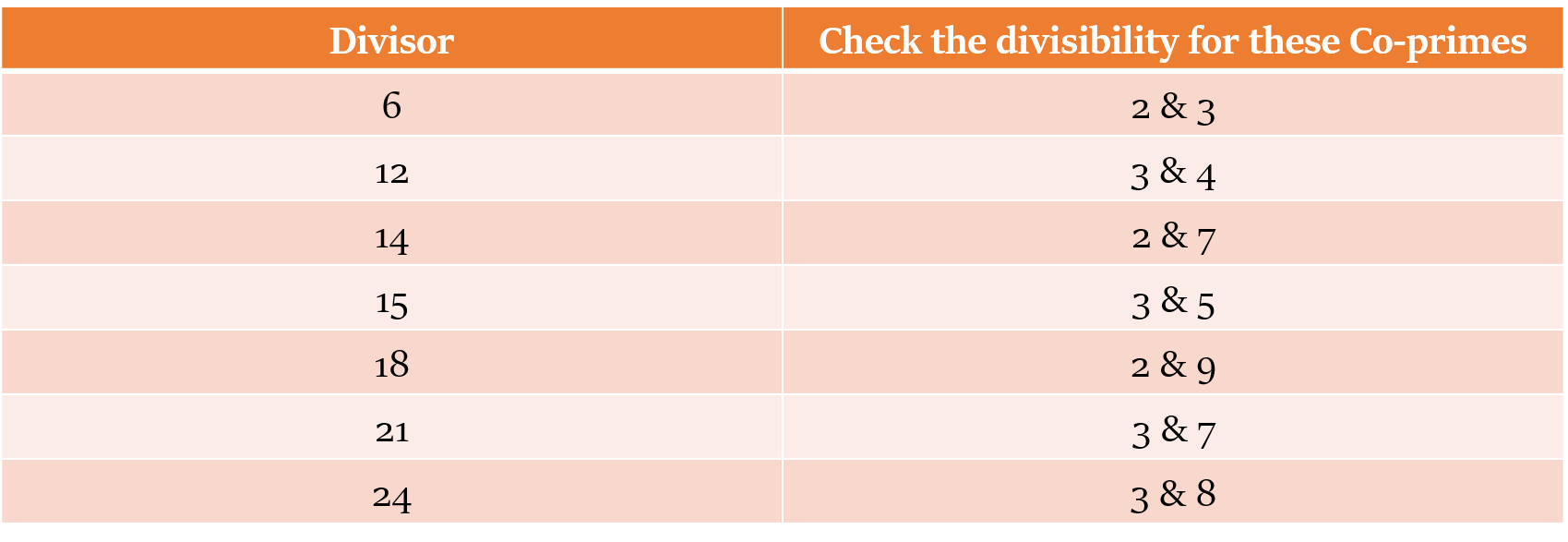

नोट

यदि कोई संख्या x और y से विभाज्य है (लेकिन x और y सह-अभाज्य नहीं हैं), तो जरूरी नहीं कि दी गई संख्या को xy से विभाज्य हो।

उदा. 36, 3 और 9 दोनों से विभाज्य है। लेकिन यह (3 × 9) = 27 से विभाज्य नहीं है (क्योंकि 3 और 9 सह-अभाज्य नहीं हैं)।

7, 13, 17, 19 और 23 से विभाज्यता (Divisibility by 7, 13, 17, 19 and 23)

इन अभाज्य संख्याओं (7, 13, 17, 19 और 23) से विभाज्यता जांचने के लिए, हम संचालिका और संक्रिया आधारित पद्धति (Operator and Operation based method) का उपयोग करेंगे।

इन भाजक में से प्रत्येक का एक विशिष्ट संचालिका (operator) और एक विशिष्ट संक्रिया (operation) होती है। इसे नीचे दी गई तालिका में दिखाया गया है:

संचालिका और संक्रिया आधारित पद्धति (Operator and Operation based method) में 3 चरण शामिल होते हैं:

• चरण 1: हम दी गई संख्या के इकाई स्थान को संबंधित संकारक (operator) से गुणा करेंगे।

• चरण 2: इसके बाद हम दी गई संख्या के शेष भाग पर संबंधित संक्रिया (घटाव या जोड़) लागू करेंगे।

• चरण 3: हम इन दो चरणों को तब तक दोहराते रहेंगे, जब तक हम यह नहीं पहचान लेते कि परिणामी अंतर भाजक का गुणज (multiple of the divisor) है या नहीं। यदि यह परिणामी अंतर भाजक का गुणज है, तो दी गई संख्या भी भाजक का गुणज होगी, अन्यथा ऐसा नहीं होगा।

आइए, कुछ उदाहरणों का उपयोग करके यह सब समझते हैं।

7 से विभाज्यता (Divisibility by 7)

ज्ञात कीजिए कि 2142, 7 का गुणज (multiple) है या नहीं।

7 के लिए, संकारक 2 है और संक्रिया घटाव है।

214 − (2 × 2) = 210
21 − (2 × 0) = 21
2 - (2 × 1) = 0

अत: 2142, 7 का गुणज है।

13 से विभाज्यता (Divisibility by 13)

ज्ञात कीजिए कि 2795, 13 का गुणज (multiple) है या नहीं।

13 के लिए, संकारक 4 है और संक्रिया जोड़ है।

279 + (4 × 5) = 299
29 + (4 × 9) = 65
6 + (4 × 5) = 26
2 + (4 × 6) = 26

26, 13 से विभाज्य है। अतः, 2795 भी 13 से विभाज्य होगा।

17 से विभाज्यता (Divisibility by 17)

ज्ञात कीजिए कि 3383, 17 का गुणज है या नहीं।

17 के लिए, संकारक 5 है और संक्रिया घटाव की है।

338 - (5 × 3) = 323
32 - (5 × 3) = 17

17, 17 से विभाज्य है। अतः, 3383 भी 17 से विभाज्य होगा।

19 से विभाज्यता (Divisibility by 19)

ज्ञात कीजिए कि 1159, 19 का गुणज है या नहीं।

19 के लिए, संकारक 2 है और संक्रिया जोड़ की है।

115 + (2 × 9) = 133
13 + (2 × 3) = 19

19, 19 से विभाज्य है। अतः, 1159 भी 19 से विभाज्य होगा।

11 से विभाज्यता (Divisibility by 11)

11 से विभाज्यता जांचने के लिए, हम वैकल्पिक डिजिटल योग पद्धति (Alternate Digital Sum method) का उपयोग करेंगे।

कोई संख्या 11 से विभाज्य होती है, यदि विषम स्थानों (odd places) पर उसके अंकों के योग और सम स्थानों (even places) पर उसके अंकों के योग का अंतर या तो 0 हो या एक ऐसी संख्या हो जो 11 से विभाज्य हो।

ज्ञात कीजिए कि 1144, 11 का गुणज है या नहीं।
विषम स्थानों पर अंकों का योग - सम स्थानों पर अंकों का योग = (1 + 4) - (1 + 4) = 0
अत: 1144, 11 से विभाज्य है।

ज्ञात कीजिए कि 82346, 11 का गुणज है या नहीं।
विषम स्थानों पर अंकों का योग - सम स्थानों पर अंकों का योग = (8 + 3 + 6) - (2 + 4) = 11.
क्यूंकि 11, 11 से विभाज्य है। अत:, 82346 भी 11 से विभाज्य होगा।

बहुपद व्यंजकों की विभाज्यता (Divisibility of polynomial expressions)

\(a^n – b^n\) की विभाज्यता (Divisibility of \(a^n – b^n\))

• \(a^n - b^n\) हमेशा a – b से विभाज्य होता है।

उदा. \(5^3 - 2^3\) = 125 - 8 = 117, जो 5 - 2 = 3 से विभाज्य है

\(5^2 - 2^2\) = 25 - 4 = 21, जो 5 - 2 = 3 से विभाज्य है

• \(a^n - b^n\), a + b से विभाज्य होता है, जब n सम हो।

उदा. \(5^4 - 2^4\) = 625 - 16 = 609, जो 5 + 2 = 7 से विभाज्य है

• \(a^n - b^n\), a + b से विभाज्य होता है, जब n विषम हो, और a + b, 2\(b^n\) का गुणनखंड हो

उदा. \(5^3 - 2^3\) = 125 - 8 = 117, जो 5 + 2 = 7 से विभाज्य नहीं है। क्योंकि 7, 2\(b^n\) = 2(\(2^3\)) का गुणनखंड नहीं है

\(6^3 - 2^3\) = 216 - 8 = 208, जो 6 + 2 = 8 से विभाज्य है। क्योंकि 8, 2\(b^n\) = 2(\(2^3\)) = 16 का गुणनखंड है

\(a^n + b^n\) की विभाज्यता (Divisibility of \(a^n + b^n\))

• \(a^n + b^n\), a + b से विभाज्य होगा, अगर n विषम हो।

उदा. \(5^3 + 2^3\) = 125 + 8 = 133, जो 5 + 2 = 7 से विभाज्य है

• \(a^n + b^n\), a – b, से विभाज्य होगा, अगर n विषम हो, और a - b, 2\(b^n\) का गुणनखंड हो

उदा. \(5^3 + 2^3\) = 125 + 8 = 133, जो 5 - 2 = 3 से विभाज्य नहीं है। क्योंकि 3, 2\(b^n\) = 2(\(2^3\)) का गुणनखंड नहीं है

\(6^3 + 2^3\) = 216 + 8 = 224, जो 6 - 2 = 4 से विभाज्य है। क्योंकि 4, 2\(b^n\) = 2(\(2^3\)) का गुणनखंड है।

• \(a^n + b^n\), a + b से विभाज्य होगा, जब n सम हो, और a + b, 2\(b^n\) का गुणनखंड हो

उदा. \(5^2 + 2^2\) = 25 + 4 = 29, जो 5 + 2 = 7 से विभाज्य नहीं है। क्योंकि 7, 2\(b^n\) = 2(\(2^3\)) का गुणनखंड नहीं है

\(6^2 + 2^2\) = 36 + 4 = 40, जो 6 + 2 = 8 से विभाज्य है। क्योंकि 8, 2\(b^n\) = 2(\(2^2\)) = 8 का गुणनखंड है