Quadratic Equations in Hindi (द्विघात समीकरण)

Overview
इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Quadratic Equations, in Hindi
द्विघात समीकरण क्या है?
यह दूसरी डिग्री के समीकरण हैं। उदाहरण के लिए, \(x^2\) + x - 2 = 0, \(x^2\) - 3y + 2 = 0
द्विघात समीकरण में चरों की संख्या के आधार पर, हम उन्हें आगे निम्न प्रकारों में विभाजित कर सकते हैं:
* एक चर के द्विघात समीकरण - जैसे की \(x^2\) + x + 1 = 0
* दो चरों के द्विघात समीकरण - जैसे की \(y^2\) + x - 22 = 0
* तीन चरों के द्विघात समीकरण इत्यादि।
एक चर के द्विघात समीकरण
\(ax^2\) + bx + c = 0 के रूप के समीकरण एक चर के द्विघात समीकरण कहलाते हैं। यहाँ, a, b, c वास्तविक संख्याएँ हैं और a ≠ 0.
उदाहरण के लिए, \(3x^2\) + 4x - 32 = 0.
संख्याएँ a, b और c इस समीकरण के गुणांक कहलाये जाते हैं।
एक चर के द्विघात समीकरण का ग्राफ़
एक चर के द्विघात समीकरण का आलेख एक परवलय (parabola) होता है।
उदाहरण के लिए, द्विघात समीकरण \(3x^2\) + 4x - 8 = 0 को ग्राफ़ पर निम्नानुसार प्लॉट किया जा सकता है:
ग्राफ़: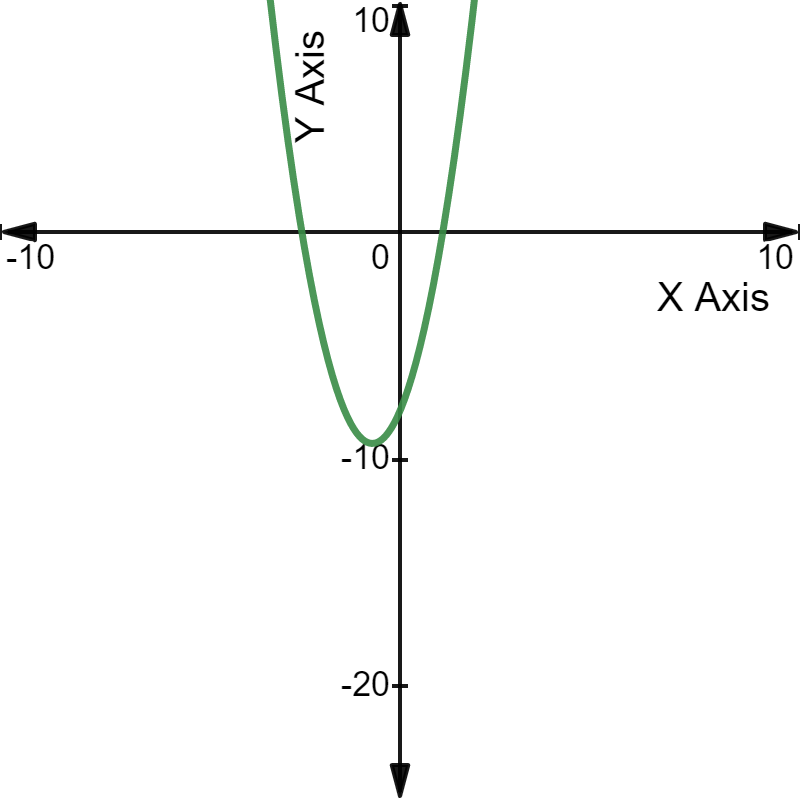
द्विघात समीकरण \(-3x^2\) + 4x + 8 = 0 को ग्राफ़ पर निम्नानुसार प्लॉट किया जा सकता है:
ग्राफ़: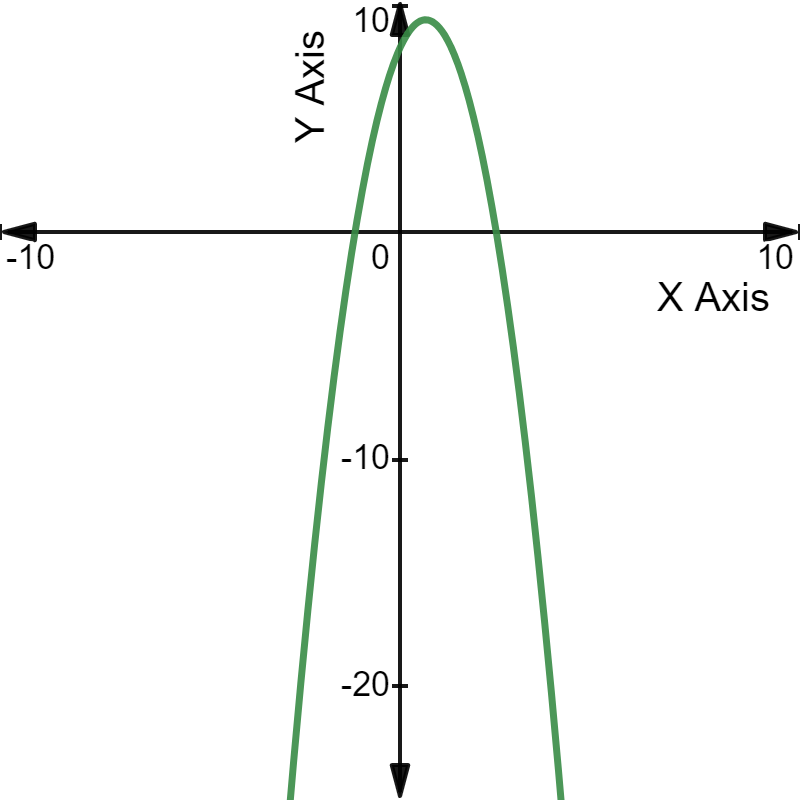
द्विघात समीकरण \(3y^2\) + 4y - 8 = 0 को ग्राफ़ पर निम्नानुसार प्लॉट किया जा सकता है:
ग्राफ़: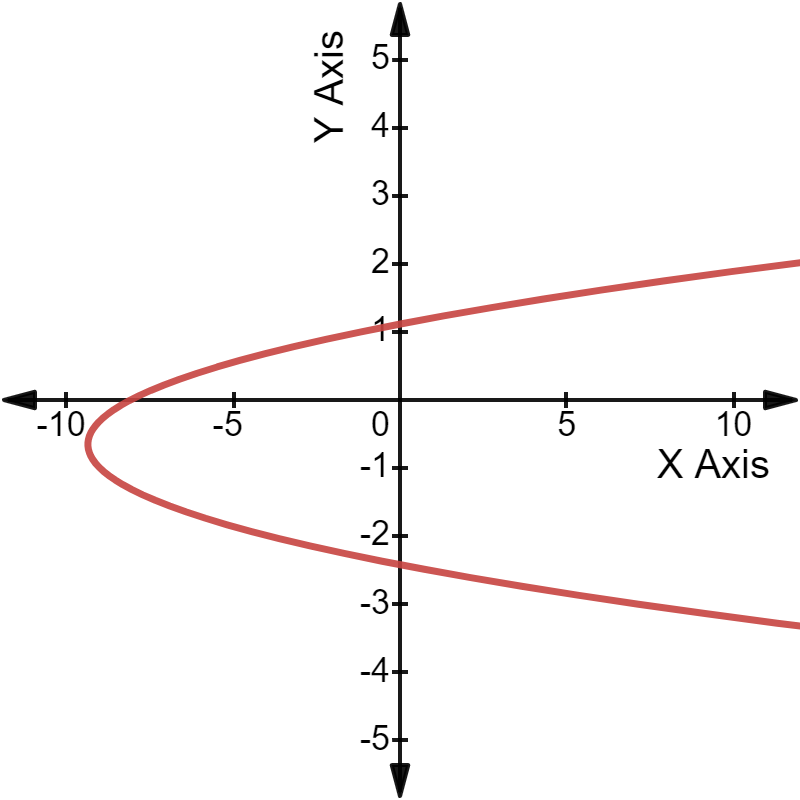
द्विघात समीकरण \(-3y^2\) + 4y + 8 = 0 को ग्राफ़ पर निम्नानुसार प्लॉट किया जा सकता है:
ग्राफ़: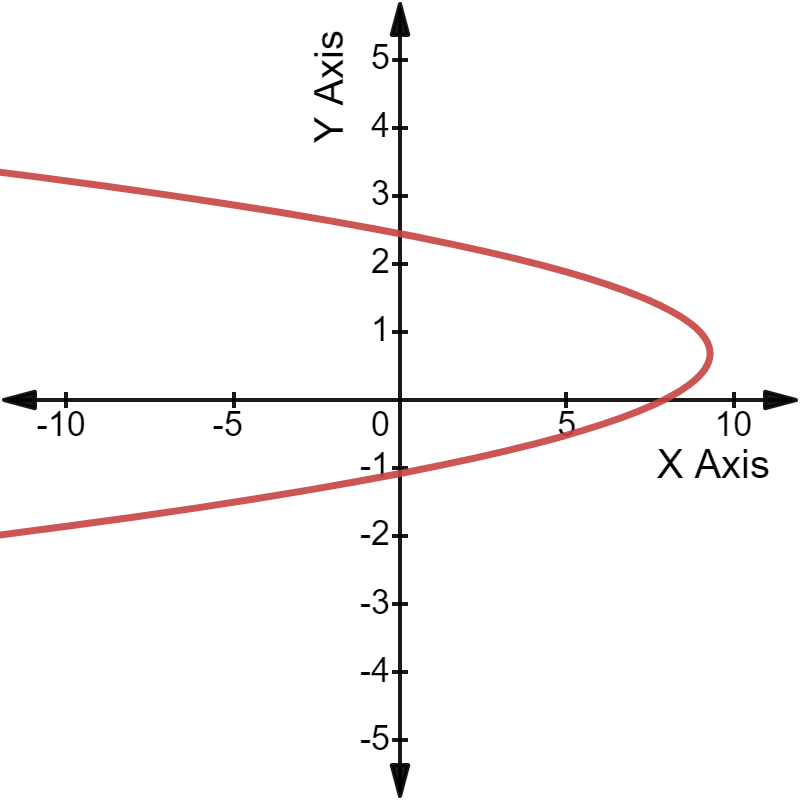
एक चर के द्विघात समीकरणों के मूल
एक चर के द्विघात समीकरण के मूल (roots) चर के वो मान होते हैं, जिस पर द्विघात व्यंजक का मान शून्य हो जाता है।
द्विघात समीकरण \(ax^2\) + bx + c = 0 के मूल, यानी x के संभावित मान, निम्न सूत्र का उपयोग करके पाए जा सकते हैं:
x = \(\frac{-b ± \sqrt{b^2 - 4ac}}{2a}\)
\(b^2 - 4ac\) को इस द्विघात समीकरण का विवेचक (discriminant) कहा जाता है, और इसे D द्वारा दर्शाया जाता है।
D का मान यह तय करता है कि द्विघात समीकरण के एक या दो मूल हैं और वे वास्तविक हैं या काल्पनिक।
D > 0
यदि D > 0, तो \(\sqrt{b^2 - 4ac}\) के दो वास्तविक मान होंगे, एक धनात्मक और दूसरा ऋणात्मक। अत: द्विघात समीकरण के दो भिन्न वास्तविक मूल होंगे।
आलेखीय शब्दों में, हम कह सकते हैं कि उस द्विघात समीकरण का परवलय X-अक्ष को दो स्थानों पर प्रतिच्छेद करेगा।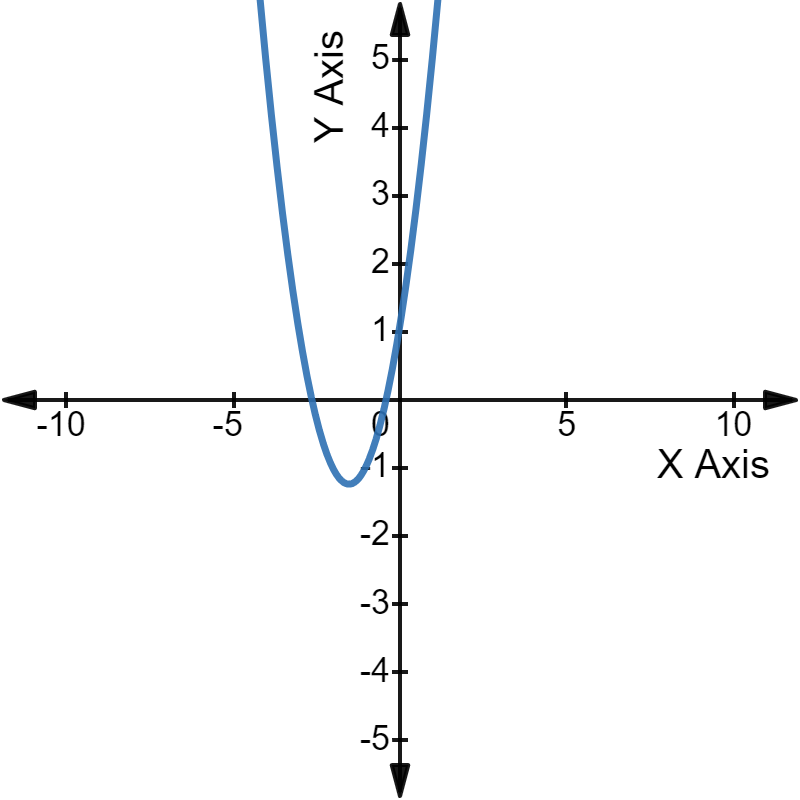
यहाँ, परवलय के x-प्रतिच्छेदन द्विघात समीकरण के हल/मूल हैं।
D = 0
यदि D = 0 है, तो \(\sqrt{b^2 - 4ac}\) का एक वास्तविक मान होगा, अर्थात 0 (शून्य)। तो, द्विघात समीकरण का केवल एक वास्तविक मूल होगा।
आलेखीय शब्दों में हम कह सकते हैं कि उस द्विघात समीकरण का परवलय X-अक्ष को केवल एक ही स्थान पर स्पर्श करेगा।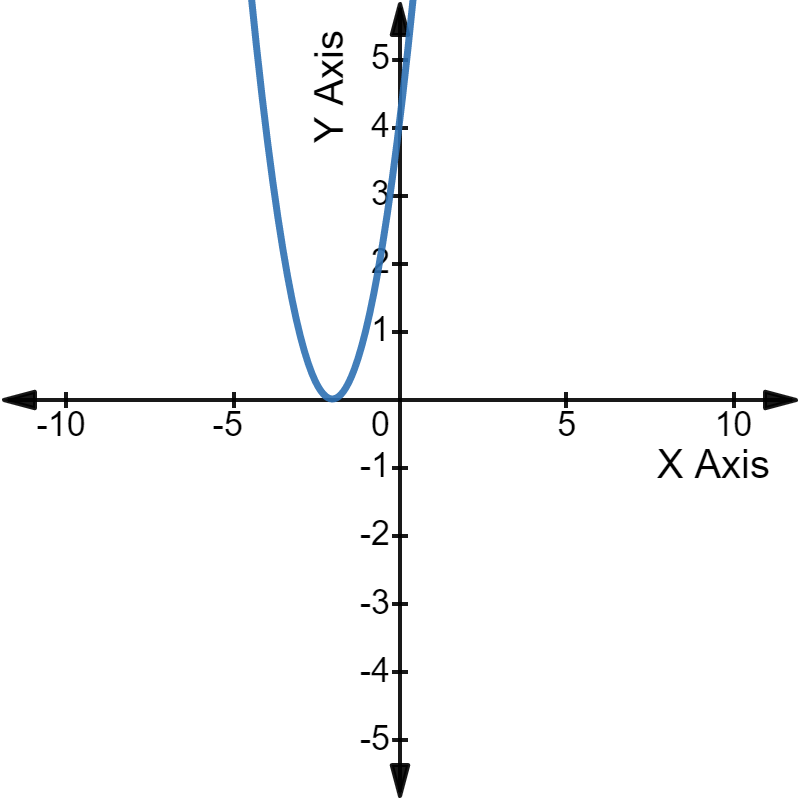
यहाँ, परवलय का x-प्रतिच्छेदन द्विघात समीकरण का हल/मूल है।
D < 0
अगर D < 0, तो \(\sqrt{b^2 - 4ac}\) का कोई वास्तविक मान नहीं होगा। अत: द्विघात समीकरण का कोई वास्तविक मूल नहीं होगा।
आलेखीय शब्दों में, हम कह सकते हैं कि उस द्विघात समीकरण का परवलय X-अक्ष को बिल्कुल भी स्पर्श या प्रतिच्छेद नहीं करेगा।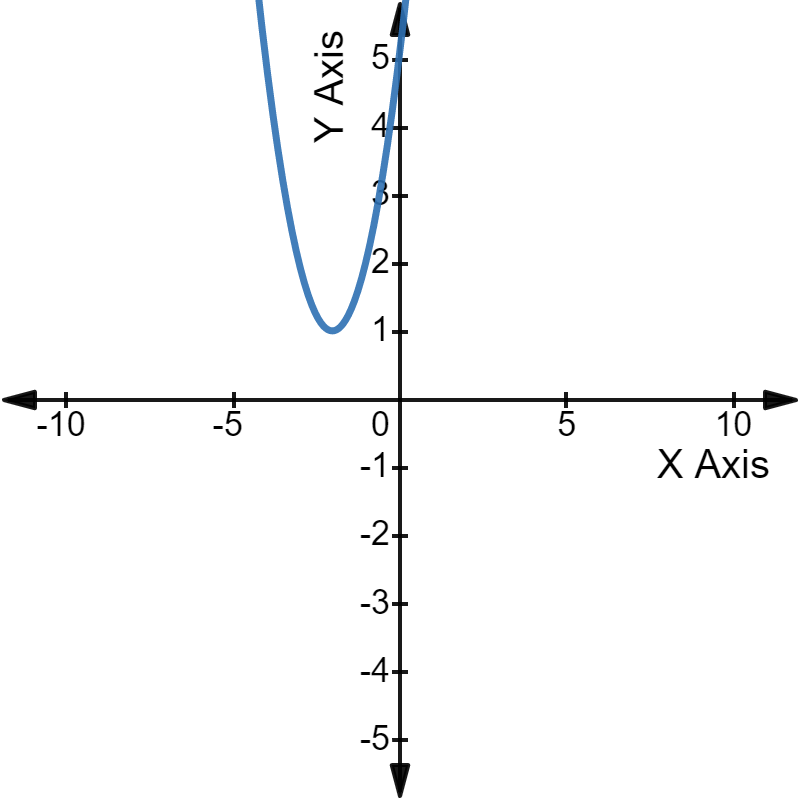
चूंकि परवलय ने X-अक्ष को छुआ तक नहीं है, इसलिए संबंधित द्विघात समीकरण का कोई वास्तविक मूल नहीं है।
द्विघात समीकरणों के गुण
गुण 1
एक चर वाले द्विघात समीकरण के 0, 1 या 2 वास्तविक मूल हो सकते हैं। इसके दो से अधिक भिन्न मूल नहीं हो सकते।
गुण 2
यदि m द्विघात समीकरण a\(x^2\) + bx + c = 0 का मूल है, तो (x - m) उस द्विघात समीकरण का एक गुणनखंड (factor) होना चाहिए।
गुण 3: मूलों का योग
यदि α और β द्विघात समीकरण a\(x^2\) + bx + c = 0 (जहाँ a ≠ 0) के मूल हैं, तो:
मूलों का योग, α + β = -\((\frac{x \hspace{1ex} का \hspace{1ex} गुणांक}{x^2 \hspace{1ex} का \hspace{1ex} गुणांक})\) = -\((\frac{b}{a})\)
गुण 4: मूलों की गुणा
यदि α और β द्विघात समीकरण a\(x^2\) + bx + c = 0 (जहाँ a ≠ 0) के मूल हैं, तो:
मूलों की गुणा, α × β = \((\frac{अचर \hspace{1ex} संख्या}{x^2 \hspace{1ex} का \hspace{1ex} गुणांक})\) = \((\frac{c}{a})\)
 नोट
नोटयदि α, β, और घन समीकरण a\(x^3\) + b\(x^2\) + cx + d = 0 (जहाँ a ≠ 0) के मूल हैं, तो:
मूलों का योग, α + β + γ = -\((\frac{x^2 \hspace{1ex} का \hspace{1ex} गुणांक}{x^3 \hspace{1ex} का \hspace{1ex} गुणांक})\) = -\((\frac{b}{a})\)
αβ + βγ + γα = \((\frac{x \hspace{1ex} का \hspace{1ex} गुणांक}{x^3 \hspace{1ex} का \hspace{1ex} गुणांक})\) = \((\frac{c}{a})\)
मूलों की गुणा, α × β × γ = -\((\frac{अचर \hspace{1ex} संख्या}{x^3 \hspace{1ex} का \hspace{1ex} गुणांक})\) = -\((\frac{d}{a})\)
जिस प्रकार द्विघात समीकरण के दो वास्तविक मूल हो सकते हैं, उसी प्रकार एक घन समीकरण के तीन मूल हो सकते हैं। लेकिन एक द्विघात समीकरण के विपरीत, एक घन समीकरण में हमेशा कम से कम एक वास्तविक मूल होता ही है। (द्विघात समीकरण में कोई वास्तविक मूल न होना भी संभव है|)
मूलों के चिह्न
अब, आइए समझते हैं कि गुणांकों के चिह्नों का उपयोग करके द्विघात समीकरण के मूलों के चिह्न कैसे ज्ञात किए जाते हैं। इसे साइन मेथड (Sign Method) कहा जाता है। यह वस्तुनिष्ठ प्रकार के प्रश्नों में बहुत उपयोगी हो सकता है।
हम द्विघात समीकरण a\(x^2\) + bx + c = 0 (जहाँ a ≠ 0) पर विचार करेंगे। सुनिश्चित करें कि a धनात्मक है। यदि यह नहीं है, तो समीकरण को -1 से गुणा करें और इसे धनात्मक बनाएं।
अब, b और c के चिह्नों की बात करें तो चार केस/मामले संभव हैं।
केस 1: b+, c+
यदि b और c दोनों धनात्मक हैं, तो दोनों मूल ऋणात्मक होंगे।
उदाहरण के लिए, द्विघात समीकरण \(x^2\) + 4x + 3 = 0 के ग्राफ़ पर एक नज़र डालें।
ग्राफ़: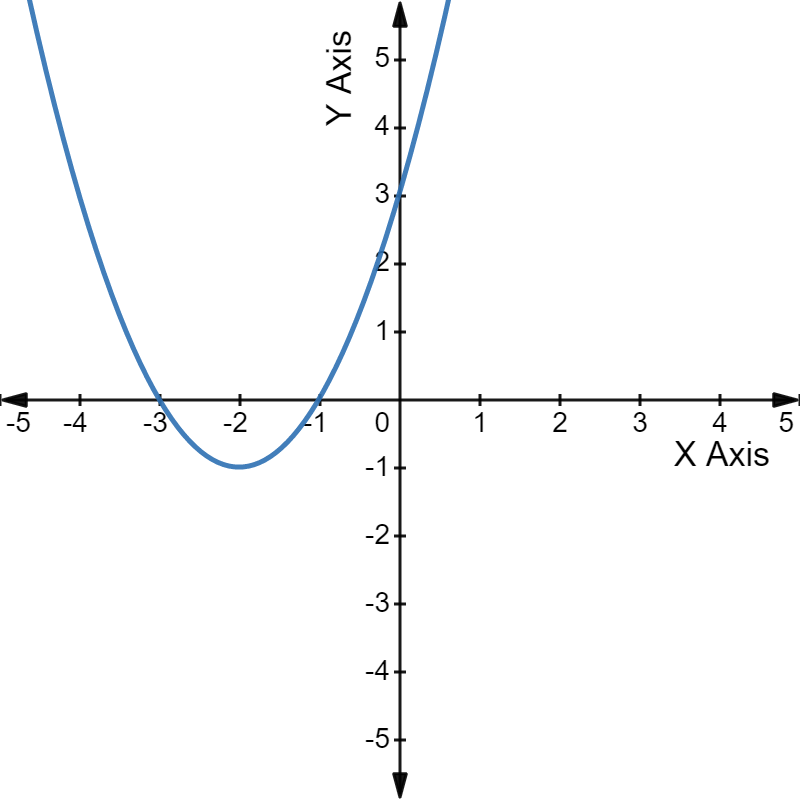 परवलय दिए गए समीकरण के दो मूलों -1 और -3 पर X-अक्ष को इंटरसेप्ट करता है।
परवलय दिए गए समीकरण के दो मूलों -1 और -3 पर X-अक्ष को इंटरसेप्ट करता है।
केस 2: b-, c-
यदि b और c दोनों ऋणात्मक हैं, तो:
- एक मूल धनात्मक होगा (बड़ी संख्या)
- एक मूल ऋणात्मक होगा (छोटी संख्या)
उदाहरण के लिए, द्विघात समीकरण \(x^2\) - 2x - 3 = 0 के ग्राफ़ पर एक नज़र डालें।
ग्राफ़: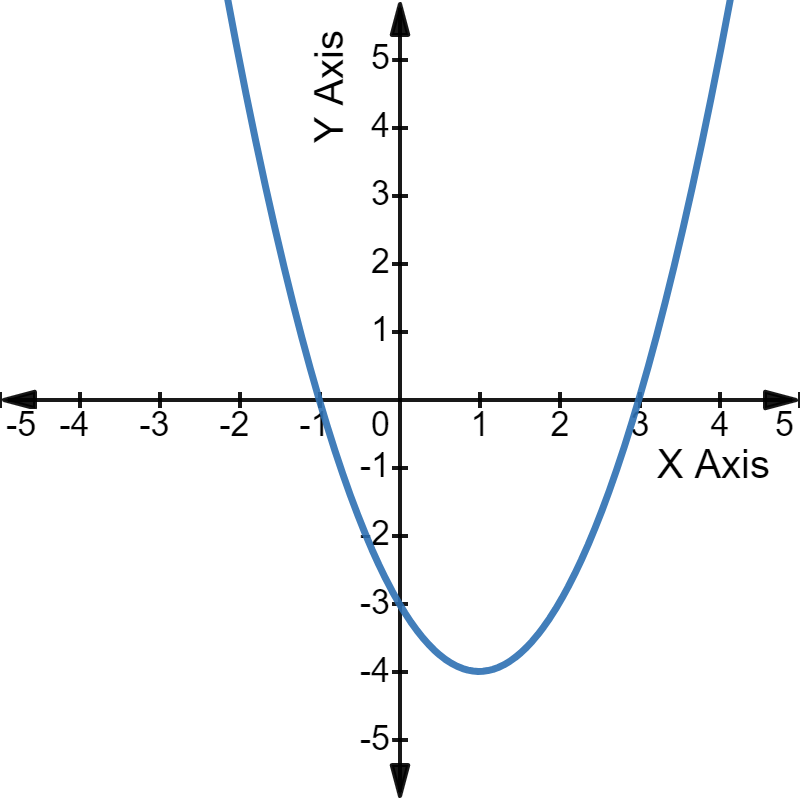 परवलय दिए गए समीकरण के दो मूलों -1 और 3 पर X-अक्ष को इंटरसेप्ट करता है।
परवलय दिए गए समीकरण के दो मूलों -1 और 3 पर X-अक्ष को इंटरसेप्ट करता है।
केस 3: b+, c-
यदि b धनात्मक है और c ऋणात्मक है, तो:
- एक मूल धनात्मक होगा (छोटी संख्या)
- एक मूल ऋणात्मक होगा (बड़ी संख्या)
उदाहरण के लिए, द्विघात समीकरण \(x^2\) + 2x - 3 = 0 के ग्राफ़ पर एक नज़र डालें।
ग्राफ़: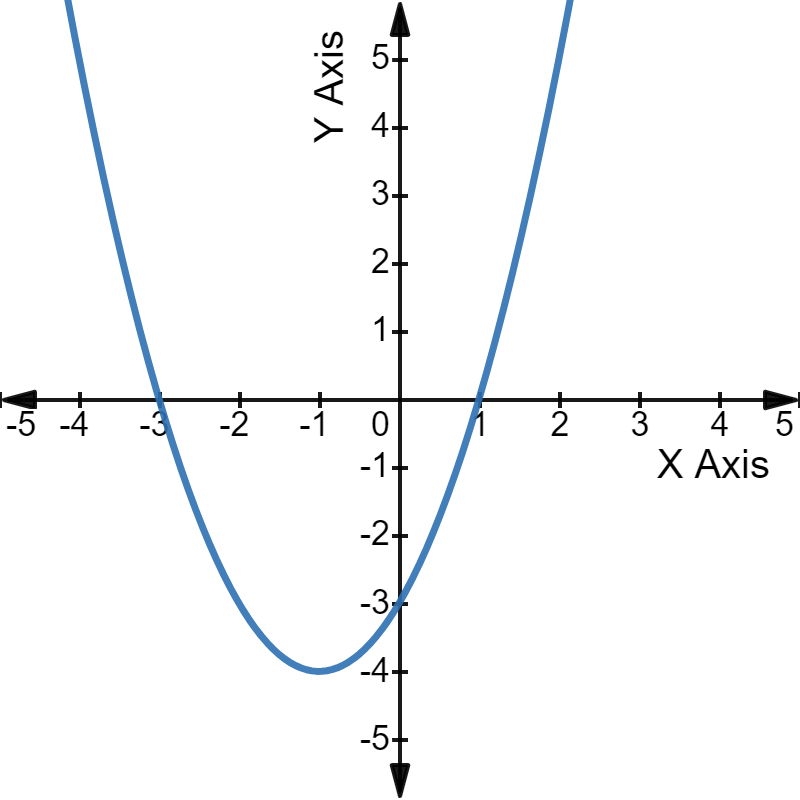 परवलय X-अक्ष को 1 और -3 पर प्रतिच्छेदित करता है, जो दिए गए समीकरण के दो मूल हैं।
परवलय X-अक्ष को 1 और -3 पर प्रतिच्छेदित करता है, जो दिए गए समीकरण के दो मूल हैं।
केस 4: b-, c+
यदि b ऋणात्मक है और c धनात्मक है, तो दोनों मूल धनात्मक होंगे।
उदाहरण के लिए, द्विघात समीकरण \(x^2\) - 5x + 6 = 0 के ग्राफ़ पर एक नज़र डालें।
ग्राफ़: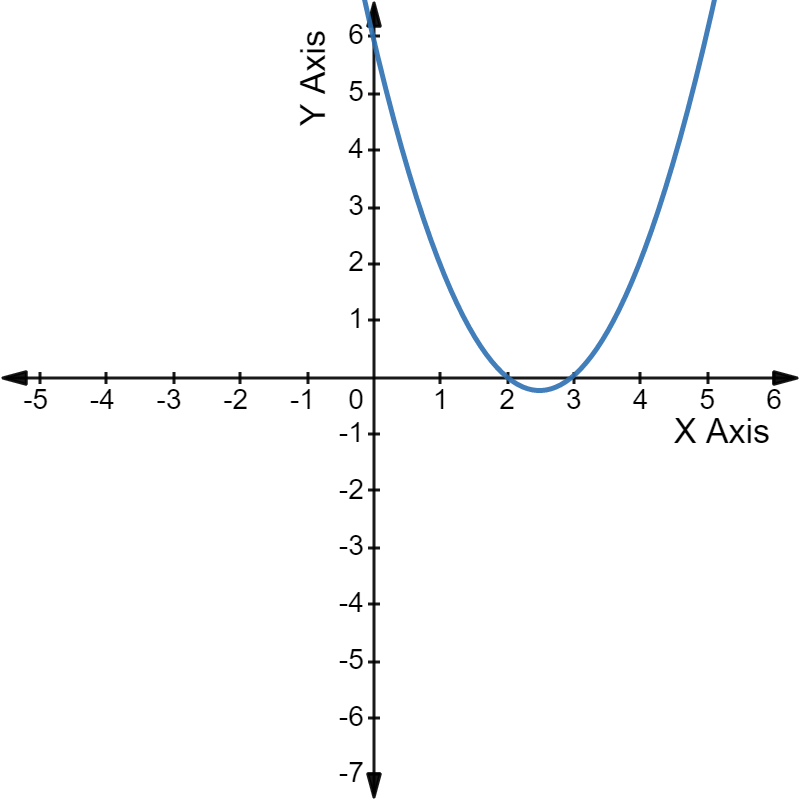 परवलय, दिए गए समीकरण के दो मूलों, 2 और 3 पर X-अक्ष को प्रतिच्छेदित करता है।
परवलय, दिए गए समीकरण के दो मूलों, 2 और 3 पर X-अक्ष को प्रतिच्छेदित करता है।
संक्षेप में:
| x का गुणांक (b) | अचर (c) | मूल α | मूल β |
|---|---|---|---|
| धनात्मक | धनात्मक | - | - |
| ऋणात्मक | ऋणात्मक | + (बड़ी संख्या) | - (छोटी संख्या) |
| धनात्मक | ऋणात्मक | + (छोटी संख्या) | - (बड़ी संख्या) |
| ऋणात्मक | धनात्मक | + | + |
द्विघात समीकरण के मूल कैसे ज्ञात करें?
द्विघात समीकरण के मूल ज्ञात करने के लिए, इसे a\(x^2\) + bx + c = 0 (जहाँ a ≠ 0) के रूप में लिखें। सुनिश्चित करें कि a धनात्मक है। यदि यह नहीं है, तो समीकरण को -1 से गुणा करें और इसे धनात्मक बनाएं।
अब दो केस/मामले सामने आ सकते हैं।
केस 1: a = 1
यदि \(x^2\) का गुणांक, अर्थात a = 1 है, तो हमारा कार्य बहुत सरल हो जाता है।
चरण 1: दो संख्याएँ, m और n ज्ञात कीजिए, ताकि इन दोनों का गुणनफल c के बराबर हो और उनका योग b के बराबर हो। (ऐसा करते समय हम चिह्नों का भी ध्यान रखेंगे)
चरण 2: अब, हम समीकरण को इस प्रकार लिख सकते हैं: (x + m) (x + n) = 0. अतः, हमारे मूल -m और -n हैं।
केस 2: a > 1
ऐसे मामले में, निम्न चरणों का पालन करें:
चरण 1: अचर पद c को a से गुणा करें। अब, दो संख्याएँ, m और n ज्ञात कीजिए, ताकि इन दोनों का गुणनफल (c × a) के बराबर हो और उनका योग b के बराबर हो। (ऐसा करते समय हम चिह्नों का भी ध्यान रखेंगे)
चरण 2: अब, हम समीकरण को इस प्रकार लिख सकते हैं: (x + m/a) (x + n/a) = 0. अतः, हमारे मूल -m/a और -n/a हैं।
आइए इस अवधारणा को स्पष्ट करने के लिए कुछ उदाहरण देखें।
प्रश्न.
समीकरण \(x^2\) + 4x + 3 = 0 के मूल ज्ञात कीजिए
हल :
दिया गया समीकरण: \(x^2\) + 4x + 3 = 0
अतः, a = 1; b = 4 and c = 3
चूँकि b और c दोनों धनात्मक हैं, तो इस समीकरण के दोनों मूल ऋणात्मक होने चाहियें।
चरण 1: हम दो ऐसी संख्याएँ मालूम करेंगे, जिनका गुणनफल c (अर्थात 3) के बराबर हो, और उनका योग b (अर्थात 4) के बराबर हो।
हम देख सकते हैं कि: 1 × 3 = 3, और 1 + 3 = 4चरण 2: तो, हम दिए गए समीकरण को इस प्रकार लिख सकते हैं: (x + 1)(x + 3) = 0.
अतः, हमारे मूल -1 और -3 होंगे।
 नोट
नोटद्विघात समीकरण \(x^2\) + 4x + 3 = 0 के ग्राफ़ पर एक नज़र डालें।
ग्राफ़: परवलय दिए गए समीकरण के दो मूलों -1 और -3 पर X-अक्ष को इंटरसेप्ट करता है।
परवलय दिए गए समीकरण के दो मूलों -1 और -3 पर X-अक्ष को इंटरसेप्ट करता है।
दिया गया समीकरण: \(x^2\) + 4x + 3 = 0
अतः, a = 1; b = 4 and c = 3
हम जानते हैं कि, द्विघात समीकरण के मूल = \(\frac{-b ± \sqrt{b^2 - 4ac}}{2a}\) = \(\frac{-4 ± \sqrt{4^2 - 4 × 1 × 3}}{2 × 1}\)
= \(\frac{-4 ± \sqrt{16 - 12}}{2}\) = \(\frac{-4 ± \sqrt{4}}{2}\) = \(\frac{-4 ± 2}{2}\) = -2 ± 1 = -1 and -3
प्रश्न.
समीकरण 2\(x^2\) - 17x + 30 = 0 के मूल ज्ञात करें
हल :
दिया गया समीकरण: 2\(x^2\) - 17x + 30 = 0
अतः, a = 2; b = -17 and c = 30
चूँकि b ऋणात्मक है, और c धनात्मक है, अतः इस समीकरण के दोनों मूल धनात्मक होने चाहियें।
चरण 1: हम दो संख्याएँ इस प्रकार प्राप्त करेंगे कि उनका गुणनफल c × a (अर्थात 30 × 2 = 60) के बराबर हो, और उनका योग b (अर्थात -17) के बराबर हो।
हम देख सकते हैं कि: (-5) × (-12) = 60, और (-5) + (-12) = -17चरण 2: तो, हम दिए गए समीकरण को इस प्रकार फिर से लिख सकते हैं: (x - 5/2)(x - 12/2) = 0, या (x - 2.5) (x - 6) = 0
अतः, हमारे मूल 2.5 और 6 होंगे।
 नोट
नोटद्विघात समीकरण 2\(x^2\) - 17x + 30 = 0 के ग्राफ़ पर एक नज़र डालें।
ग्राफ़: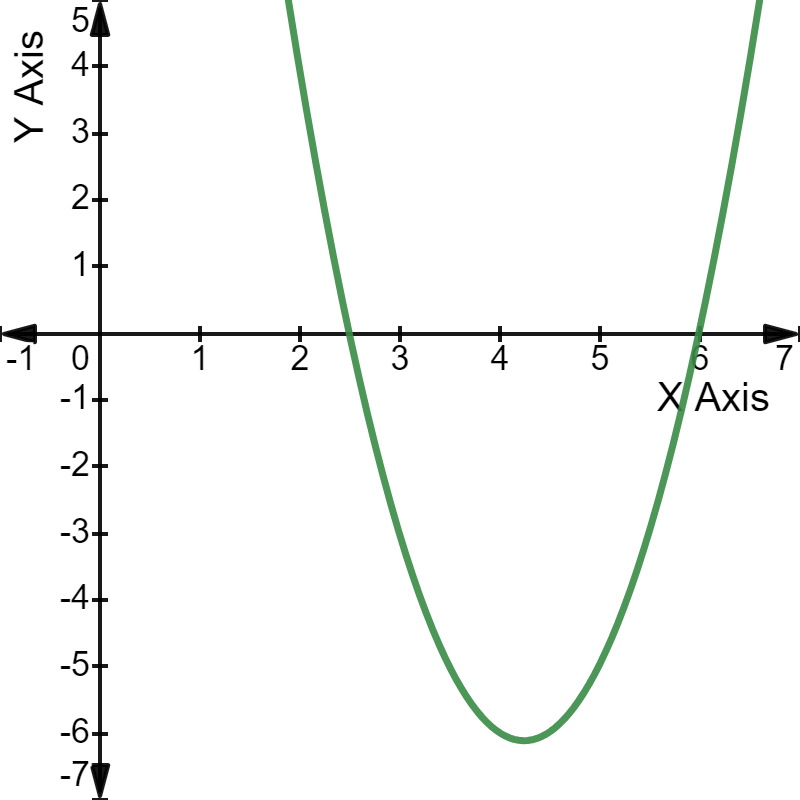 परवलय X-अक्ष को 2.5 और 6 पर प्रतिच्छेदित करता है, जो दिए गए समीकरण के दो मूल हैं।
परवलय X-अक्ष को 2.5 और 6 पर प्रतिच्छेदित करता है, जो दिए गए समीकरण के दो मूल हैं।
दिया गया समीकरण: 2\(x^2\) - 17x + 30 = 0
अतः, a = 2; b = -17 and c = 30
हम जानते हैं कि, द्विघात समीकरण के मूल = \(\frac{-b ± \sqrt{b^2 - 4ac}}{2a}\) = \(\frac{17 ± \sqrt{(-17)^2 - 4 × 2 × 30}}{2 × 2}\)
= \(\frac{17 ± \sqrt{289 - 240}}{4}\) = \(\frac{17 ± \sqrt{49}}{4}\) = \(\frac{17 ± 7}{4}\)
= 24/4 and 10/4, i.e. 6 and 2.5
comments powered by Disqus