गणित में सदिशों का परिचय (Vectors in Hindi)

Overview

इस लेख में हम गणित के एक महत्त्वपूर्ण अध्याय के बारे में जानेंगे - Vectors, in Hindi

गणित में सदिश क्या होते हैं?

सदिश (या वेक्टर) वे चीज़ें हैं जिन्हें एक तीर द्वारा दर्शाया जाता है। उनके पास निम्नलिखित दोनों होते हैं:

• परिमाण (Magnitude) - तीर की रेखा की लंबाई से निरूपित होता है।
• दिशा (Direction) - तीर के सिर से निरूपित होता है।
  

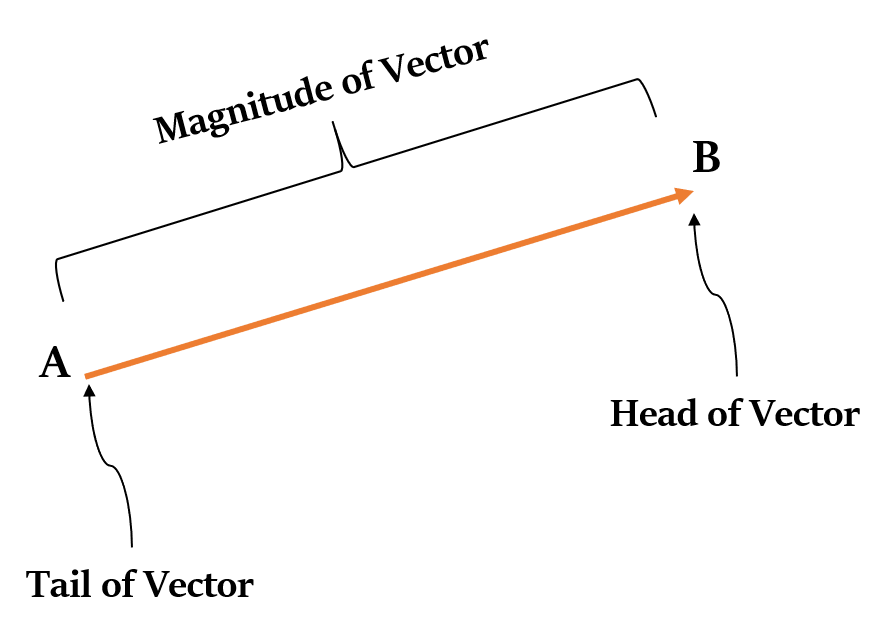
गणित में सदिशों को यूक्लिडियन सदिश (Euclidean vectors), ज्यामितीय सदिश (Geometric vectors) या स्थानिक सदिश (Spatial vectors) के रूप में भी जाना जाता है।

नोट

वैक्टर (Vectors) के विपरीत, स्केलर्स (Scalars) में केवल परिमाण होता है, कोई दिशा नहीं होती है। उदाहरण के लिए, गति (Speed) एक अदिश राशि है, जबकि वेग (Velocity) एक सदिश राशि है। वेग, गति और दिशा दोनों से मिलकर बनता है।

दो अदिश के बराबर होने के लिए, बस उनका परिमाण समान होना चाहिए।

परन्तु दो सदिश केवल तभी बराबर होते हैं जब उनके परिमाण और दिशा दोनों समान हों।

वेक्टर को उसके नाम के ऊपर एक तीर लगाकर दर्शाया जाता है, जैसे की \(\overrightarrow{a}\)

उल्टा वेक्टर (Reverse Vector)

किसी दिए गए वेक्टर \(\overrightarrow{a}\) का उल्टा वेक्टर होगा -\(\overrightarrow{a}\)। इसका परिमाण मूल वेक्टर के समान होगा, लेकिन दिशा विपरीत होगी।

वैक्टर के घटक (Components of Vectors)

x-y तल में एक वेक्टर के दो घटक होते हैं:

• क्षैतिज घटक
• लंबवत घटक

सदिशों से संबंधित प्रश्नों को हल करते समय, हम अक्सर उन सदिशों को उनके x और y घटकों में तोड़ देते हैं। इससे हमारा काम बहुत आसान हो जाता है।

यदि हमारे पास एक सदिश \(\overrightarrow{a}\) है, जो क्षैतिज X-अक्ष के साथ θ का कोण बनाता है, तो:

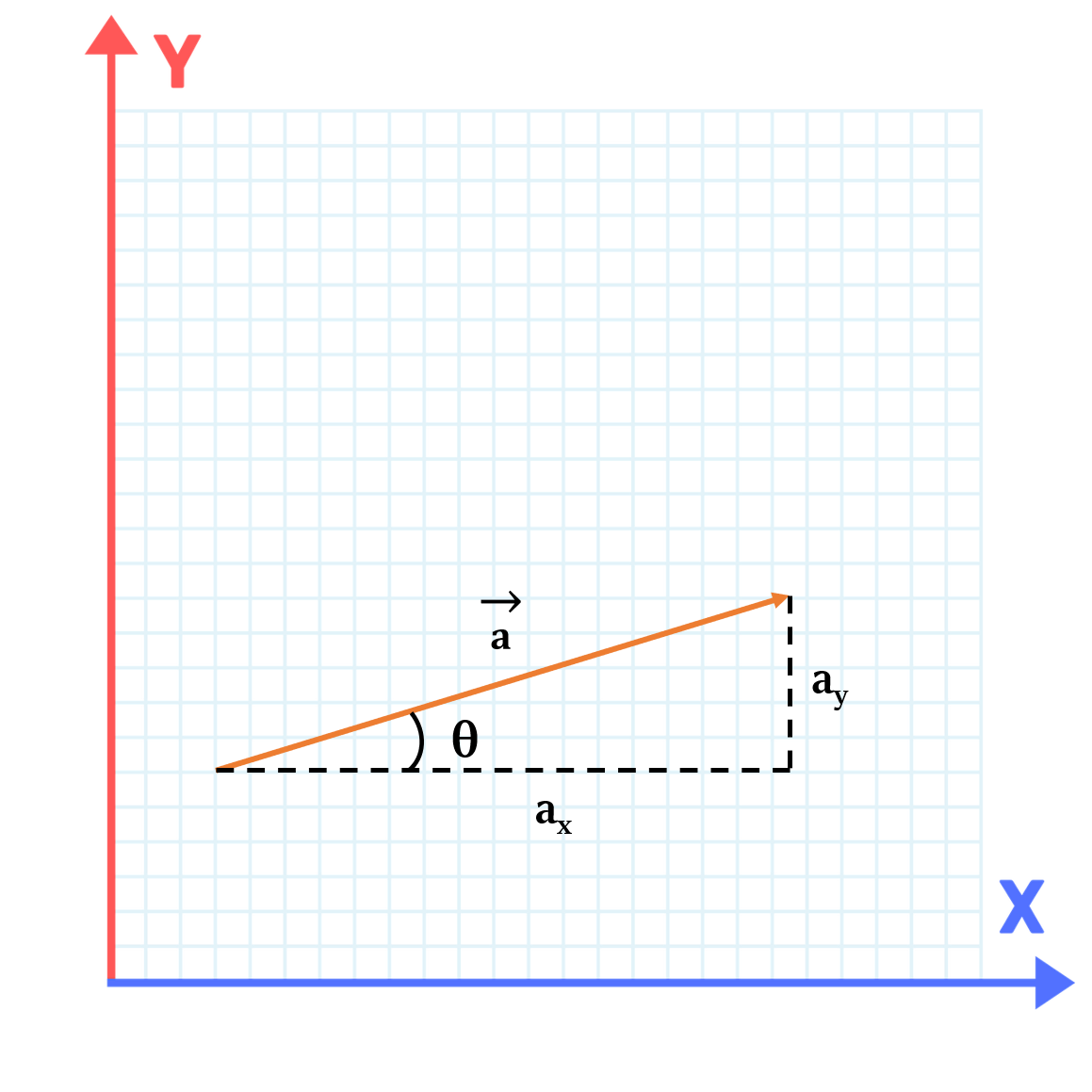
* वेक्टर का क्षैतिज घटक, \(a_x\) = a cos θ
* वेक्टर का लंबवत घटक, \(a_y\) = a sin θ

नोट

tan θ = \(\frac{a_y}{a_x}\)

वेक्टर का परिमाण (Magnitude of Vector)

वेक्टर का परिमाण उस वेक्टर की लंबाई होती है। इसे दिए गए सदिश के दोनों ओर दो लंबवत रेखाओं द्वारा दर्शाया जाता है, जैसे की \(\left\lVert a \right\rVert\)

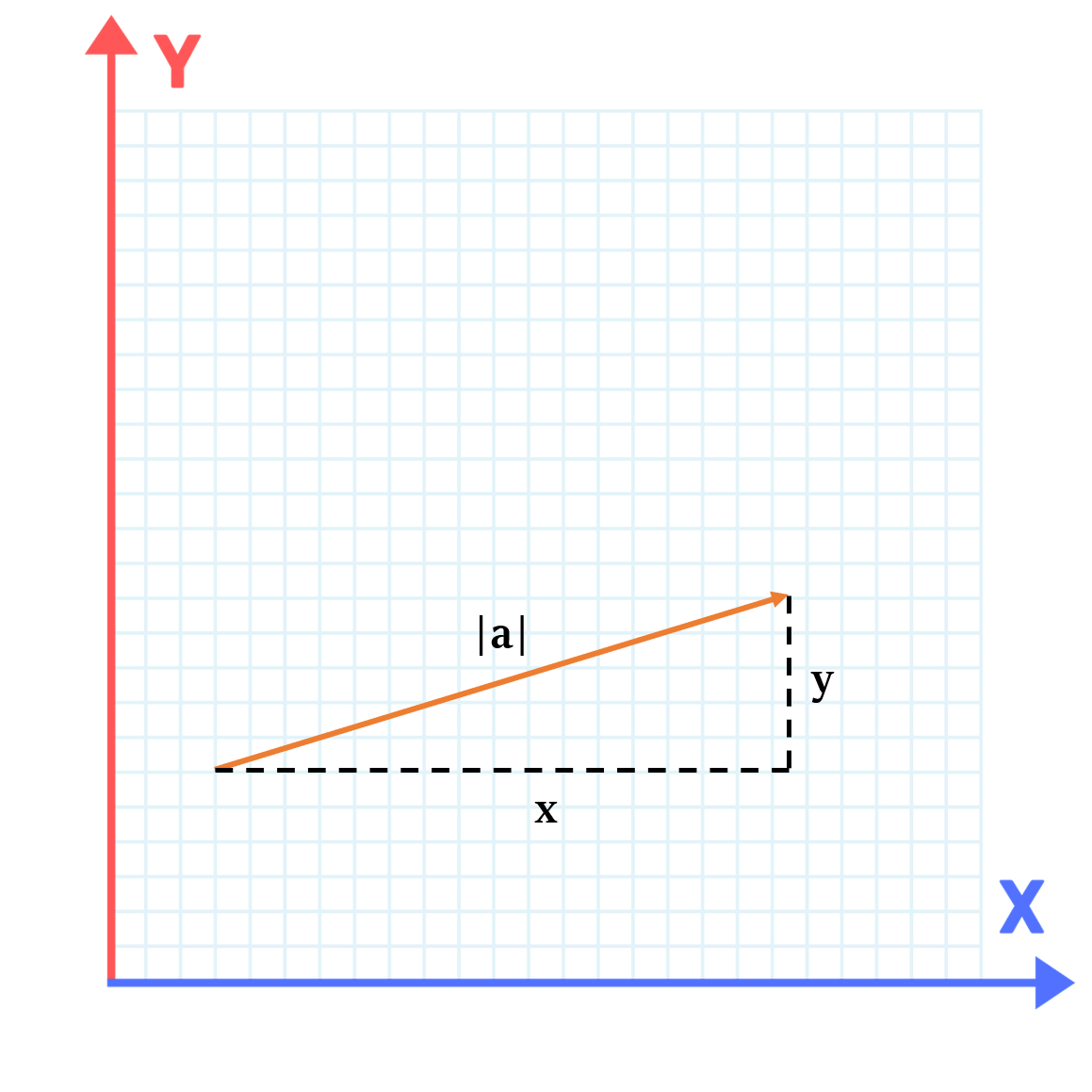
\(\left\lVert a \right\rVert = √(x^2 + y^2)\)

नोट

हम यहां डबल बार का उपयोग करते हैं, ताकि निरपेक्ष मान (absolute value) के साथ भ्रमित न हों, जहां हम सिंगल बार का उपयोग करते हैं, अर्थात |a|

नोट

वेक्टर का परिमाण ज्ञात करने के लिए आप निम्नलिखित कैलकुलेटर का उपयोग कर सकते हैं:

वेक्टर का परिमाण (Magnitude of a Vector)

इकाई वेक्टर (Unit Vector)

यदि किसी सदिश की इकाई लंबाई है, अर्थात उसका परिमाण एक के बराबर है, तो इसे एक इकाई सदिश कहा जाता है। यह वेक्टर के नाम के ऊपर एक टोपी द्वारा दर्शाया जाता है, जैसे की \(\hat{a}\)

एक वेक्टर का सामान्यीकरण (Normalising a vector) किसी दिए गए वेक्टर के यूनिट वेक्टर को खोजने की प्रक्रिया है। यूनिट वेक्टर को खोजने के लिए, हमें दिए गए वेक्टर को उसके परिमाण से विभाजित करने की आवश्यकता होती है।

अतः, \(\hat{a} = \frac{a}{\left\lVert a \right\rVert}\)

हम यूनिट वेक्टर का उपयोग तब करते हैं, जब हमें केवल वेक्टर की दिशा में रुचि होती है।

शून्य वेक्टर (Zero Vector)

यदि किसी सदिश की कोई लंबाई नहीं है, अर्थात इसका परिमाण शून्य के बराबर है, तो इसे शून्य सदिश कहा जाता है। इसे \(\overrightarrow{0}\), या 0 से दर्शाया जाता है।

शून्य सदिश के साथ किसी भी अन्य सदिश का योग उस सदिश में ही परिणत होगा। यानी, \(\overrightarrow{a} + \overrightarrow{0} = \overrightarrow{a}\)

नोट

शून्य सदिश को सामान्यीकृत (normalized) नहीं किया जा सकता, अर्थात हम शून्य सदिश का इकाई सदिश नहीं खोज सकते।

सदिशीय संक्रियाएं (Operations on Vectors)

हम वैक्टर पर जोड़, घटाव, गुणा जैसी संक्रियाएं (ऑपरेशन) कर सकते हैं।

सदिशों का जोड़ (Addition of Vectors)

दो वैक्टर \(\overrightarrow{a}\) और \(\overrightarrow{b}\) जोड़ने के लिए, हम ग्राफिकल विधि का उपयोग कर सकते हैं।

ऐसा करने के लिए, हम दो वेक्टर्स को इस तरह से रखते हैं कि एक वेक्टर की पूंछ दूसरे वेक्टर के सिर को छू रही हो।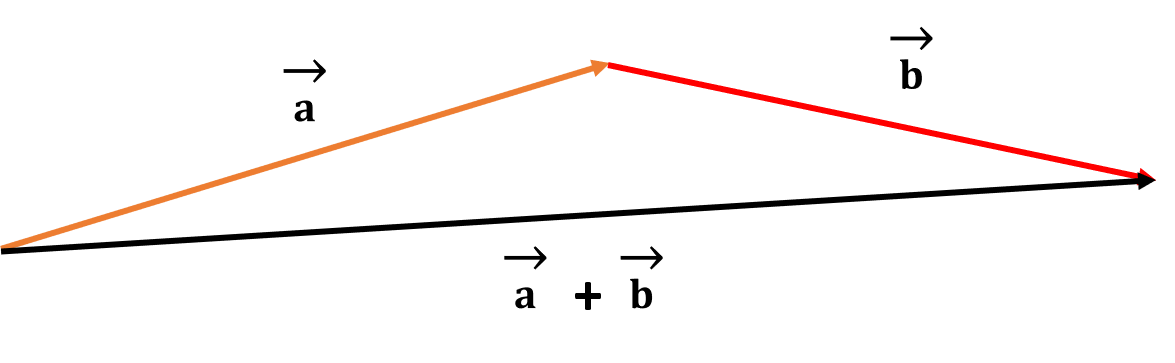

जैसा कि ऊपर दिखाया गया है, उनका योग \(\overrightarrow{a} + \overrightarrow{b}\) वो वेक्टर होगा, जो दूसरे वेक्टर के शीर्ष के साथ पहले वेक्टर की पूंछ को जोड़ता है।

नोट

वेक्टर्स जोड़ने के लिए आप निम्नलिखित कैलकुलेटर का उपयोग कर सकते हैं:

वेक्टर जोड़ (Vector addition)

नोट

सदिश जोड़ के कम्यूटेटिव नियम (commutative law of addition) का पालन करते हैं, अर्थात \(\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}\)

सदिश जोड़ के साहचर्य नियम (associative law of addition) का भी पालन करते हैं, अर्थात \((\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})\)

सदिशों का घटाव (Subtraction of Vectors)

सदिशों का घटाव, सदिशों के योग के समान है। यहां, हम घटाए जा रहे वेक्टर के रिवर्स वेक्टर को जोड़ते हैं।

यानी, \(\overrightarrow{a} - \overrightarrow{b} = \overrightarrow{a} + \overrightarrow{(-b)}\)

सदिशों का गुणन (Multiplication of Vectors)

वेक्टर्स के मामले में विभिन्न प्रकार के गुणन संभव हैं। आइए उन्हें देखते हैं।

स्केलर गुणन (Scalar Multiplication)

जब एक सदिश (vector) को किसी अदिश राशि (scalar) से गुणा किया जाता है, तो इसे अदिश गुणन / स्केलर गुणन कहते हैं।

स्केलर गुणन सदिश के परिमाण को बदल सकता है, अर्थात यह सदिश को छोटा कर सकता है या इसे बड़ा कर सकता है।

धनात्मक संख्याओं के साथ अदिश गुणन सदिश की दिशा नहीं बदलेगा। परन्तु, किसी नकारात्मक अदिश के साथ अदिश गुणन वेक्टर की दिशा को उलट देगा।

उदाहरण के लिए, 3 . \(\overrightarrow{a} = \overrightarrow{3a}\)
0 . \(\overrightarrow{a} = \overrightarrow{0}\) (बाईं ओर शून्य संख्या 0 है, जबकि दाईं ओर शून्य सदिश 0 है।)
1 . \(\overrightarrow{a} = \overrightarrow{a}\)
(-1) . \(\overrightarrow{a} = \overrightarrow{(-a)}\)

नोट

यदि \(\overrightarrow{a}\) and \(\overrightarrow{b}\) दो सदिश हैं, और \(S_1\) & \(S_2\) अदिश राशि हैं, तो:
\(S_1 (\overrightarrow{a} + \overrightarrow{b}) = S_1 \overrightarrow{a} + S_1 \overrightarrow{b}\)
\((S_1 + S_2) \overrightarrow{a} = S_1 \overrightarrow{a} + S_2 \overrightarrow{a}\)

वेक्टर गुणन (Vector Multiplication)

जब हम दो या दो से अधिक सदिशों को गुणा करते हैं, तो इसे सदिश गुणन कहते हैं।

वेक्टर गुणन दो प्रकार के होते हैं:

• क्रॉस गुणन (सदिश गुणनफल या अन्योन्य गुणन, Cross Product) - इसका परिणाम कोई वेक्टर होता है
• डॉट गुणन (अदिश गुणनफल या बिन्दु गुणनफल, Dot Product) - इसका परिणाम कोई अदिश मात्रा होती है

आइए इनका विस्तार से अध्ययन करें।

वेक्टरों का सदिश गुणनफल (Cross Product of Vectors )

जैसा कि पहले ही उल्लेख किया गया है, दो वैक्टरों के क्रॉस उत्पाद के परिणामस्वरूप एक वेक्टर मात्रा प्राप्त होती है (यानी ऐसी मात्रा जिसमें परिमाण और दिशा दोनों होती है)। हम इसे निरूपित करने के लिए क्रॉस चिन्ह (×) का उपयोग करते हैं।

उदाहरण के लिए, दो वेक्टर्स के क्रॉस गुणन को \(\overrightarrow{a} × \overrightarrow{b}\) के रूप में दर्शाया जाएगा।

जैसे की: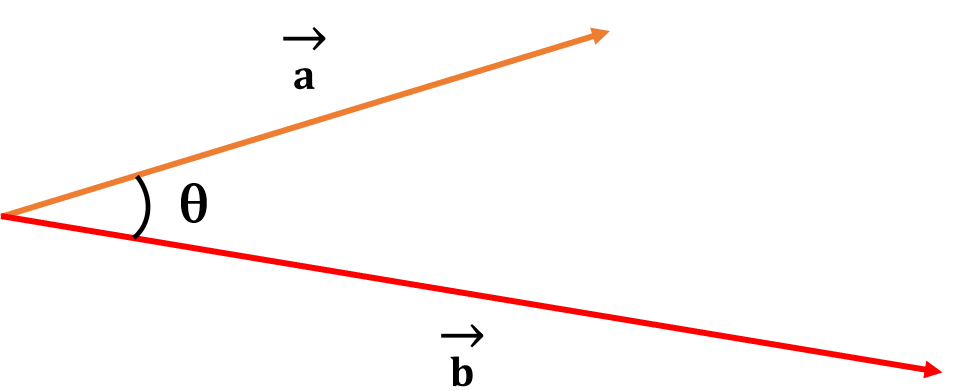

\(\overrightarrow{a} × \overrightarrow{b} = \left\lVert a \right\rVert \left\lVert b \right\rVert sin θ \hat{n}\)

जहां \(\left\lVert a \right\rVert\) और \(\left\lVert b \right\rVert\) क्रमशः \(\overrightarrow{a}\) और \(\overrightarrow{b}\) वेक्टर्स के परिमाण हैं, और θ उन दो वैक्टरों के बीच का कोण है।

\(\hat{n}\) एक इकाई वेक्टर है। यह इन दो वैक्टरों के गुणन की दिशा को दर्शाता है।

नोट

वैक्टर के क्रॉस गुणन के लिए आप निम्नलिखित कैलकुलेटर का उपयोग कर सकते हैं:

क्रॉस प्रोडक्ट कैलकुलेटर (Cross product calculator)

वेक्टरों का अदिश गुणनफल (Dot Product of Vectors )

जैसा कि पहले ही उल्लेख किया गया है, दो वेक्टरों के डॉट गुणनफल का परिणाम हमेशा एक अदिश राशि होती है (अर्थात एक ऐसी मात्रा जिसमें केवल परिमाण होता है, कोई दिशा नहीं होती है)। इसे निरूपित करने के लिए हम बिंदु चिह्न (.) का प्रयोग करते हैं।

उदाहरण के लिए, दो वेक्टरों के डॉट गुणनफल को इस प्रकार दर्शाया जाएगा \(\overrightarrow{a} . \overrightarrow{b}\)

\(\overrightarrow{a} . \overrightarrow{b} = \left\lVert a \right\rVert \left\lVert b \right\rVert cos θ\)

नोट

वैक्टर के डॉट गुणनफल के लिए आप निम्नलिखित कैलकुलेटर का उपयोग कर सकते हैं:

अदिश गुणनफल (Dot product)

नोट

हम किसी भी समन्वय प्रणाली के संदर्भ में या उसके बिना वैक्टर, और वेक्टर संक्रियाओं (जोड़, घटाव और अदिश गुणन) का वर्णन कर सकते हैं।